外れ値の判定－距離の基準はいつも同じか?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

統計を行う際には、母集団から取り出したデータが様々な分布を見せる。それらのデータの分布図を描いたり、平均値や標準偏差の値を計算したりして、母集団の特徴を把握しようと試みる。そこで、問題になるのが、外れ値である。これは他のデータと比較して、突出して大きい、もしくは小さい値を示すデータである。例えば、あるデータが他のデータに比べて特に大きい場合、これを外れ値として、他のデータから除外すべきかどうか検討する。しかし、この検討は容易ではない。

統計の担当者が、「このデータは、どう見ても他のデータとは値がかけ離れているから、外れ値とみなす」などと、主観的に判断する訳にはいかない。そこで、客観的に、外れ値を判断するための方法がいろいろと考えられている。

まず、平均と標準偏差を用いる方法がある。問題のデータを除外して、残りのデータから平均と標準偏差の値を計算してみる。問題のデータが平均から標準偏差の値の3倍以上離れていたら、外れ値と判断する、という方法である。しかし、この方法では、全体のデータの数が少ない場合には、平均の値が安定せず、外れ値の判断に支障が出てしまう。

別の方法として、データの四分位点を用いる方法がある。データを大きい方から順番に並べたときに、全体の四分の一と、四分の三にあたるデータが定まる。この2つのデータを上側四分位点、下側四分位点と呼ぶ。この2つの四分位点の差の1.5倍を上側四分位点に足して、それよりも大きなデータは外れ値と判断する。同様に、差の1.5倍を下側四分位点から引いて、それよりも小さなデータを外れ値と判断する。しかし、この方法では、データが中央に密集している場合には、2つの四分位点の差が小さくなり、外れ値が多発してしまう。

このように、外れ値の判断を機械的に行うことは難しい。データの分布図を描いてみて、そのデータが群団全体からどのように外れているかを見ることが、判断のための王道となる。

ここまでは、データが1つの値からなる場合の話であった。次に、データが2つの値からなる場合を考えてみよう。例として、身長と体重の平均が同じである2つの成人の集団について、横軸に身長、縦軸に体重をとって、データの分布図を描いてみる。

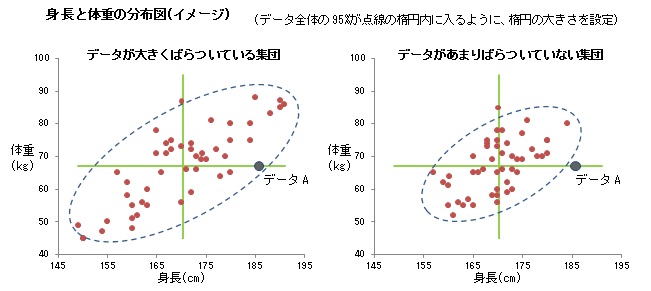
身長と体重の分布図(イメージ)　データが大きくばらついている集団／データがあまりばらついていない集団

図のデータAは、両方の集団に含まれている同一人物で、身長は平均よりもだいぶ高いが、体重は平均と同じである。このとき、それぞれの集団で、データAは、外れ値と判断すべきだろうか。このような場合、データの平均の位置(図の十字線の交点)から見て、このデータが、他のデータに比べて、どのくらい離れた場所に位置するのかを考えなくてはならない。

そのために、平均からの距離を定義して、その距離が一定以上ある場合に外れ値と判定する。図では、点線の傾いた楕円が、平均から等距離にある位置を表している。この点線の外側にあるデータを、外れ値と判定することになる。こうすると、楕円の大きさをどのように設定するか、が残された問題となる。図では、データ全体の95%が点線の楕円内に入るように楕円の大きさを設定した。この結果、データAは、データが大きくばらついている集団では外れ値ではないが、データがあまりばらついていない集団では外れ値と判断された。

このような距離は、通常の概念と異なり、データの分布具合に応じて変化する。この距離は、最初に提唱したインドの統計学者の名前をとって、「マハラノビス距離」と呼ばれている。通常は絶対的な基準である距離という概念が、統計上では、相対的な尺度になる。

外れ値の判断には、集団の中での相対的な位置関係が重要となる。そのために、統計では、距離という概念まで、相対的なものに定義し直してしまう。このことは、無機質で硬直的なイメージのある統計の裏に潜む、柔軟性を表しているように感じられるが、いかがだろうか。

日付	タイトル	執筆者	媒体
2025/03/25	産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している	篠原拓也	基礎研レター
2025/03/18	気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?	篠原拓也	基礎研レター
2025/03/11	国民負担率 24年度45.8%の見込み－高齢化を背景に、欧州諸国との差は徐々に縮小	篠原拓也	研究員の眼
2025/03/04	サイバーリスクのモデリング－相互に接続されたシステミックリスクをどうモデリングする?	篠原拓也	保険・年金フォーカス

日付

タイトル

執筆者

媒体

2025/03/25

産業クラスターを通じた脱炭素化－クラスターは温室効果ガス排出削減の潜在力を有している

篠原拓也

基礎研レター

2025/03/18

気候変動:アクチュアリースキルの活用－「プラネタリー・ソルベンシー」の枠組みに根差したリスク管理とは?

篠原拓也

基礎研レター