- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか-
コラム
2016年09月06日

文字サイズ
- 小
- 中
- 大
はじめに
人間の直感が非常に役に立つことは理解されるが、時として、この直感が数学的には正しくないことがあることは有名な話である。今回は、そうしたケースを2つ紹介したい。
誕生日のパラドックス
一番有名なのは、「誕生日のパラドックス」と呼ばれているものである。具体的には、「現在1つの部屋にn人の人がいるとする。この時に、誕生日が同じ人がいる確率はいくらか。」という問題である。あるいは「何人の人がいれば、その中で誕生日が同じ人がいる確率が50%以上になるのか。」という問題である。
これに対する答えについては、一般的に多くの人は、直感的に、相当多くの人数を想定してしまう。極端なことを言えば、365日の1/2の183人が必要だと思う人もかなりいると思われる。
ところが、この答えは23人ということになる。23人の人がいれば、少なくとも誕生日が同じ一組が存在する確率が50%を超えることになる。これは、数学的に極めて簡単に証明できる。
n人の誕生日が全て異なる確率を p(n) とする。
2人目が1人目と異なる誕生日である確率は、364/365 。3人目が1人目及び2人目と異なる誕生日である確率は 363/365 。同様に4人目は 362/365、…、n人目は (365-n+1)/365 となる。従って、n人の誕生日が全て異なる確率は、以下の通りとなる。
これに対する答えについては、一般的に多くの人は、直感的に、相当多くの人数を想定してしまう。極端なことを言えば、365日の1/2の183人が必要だと思う人もかなりいると思われる。
ところが、この答えは23人ということになる。23人の人がいれば、少なくとも誕生日が同じ一組が存在する確率が50%を超えることになる。これは、数学的に極めて簡単に証明できる。
n人の誕生日が全て異なる確率を p(n) とする。
2人目が1人目と異なる誕生日である確率は、364/365 。3人目が1人目及び2人目と異なる誕生日である確率は 363/365 。同様に4人目は 362/365、…、n人目は (365-n+1)/365 となる。従って、n人の誕生日が全て異なる確率は、以下の通りとなる。
となり、n=23の場合に、この数値は 0.507 となって、50%を超えることになる。
同じ考え方により、41人の人がいれば、90%以上の確率で、70人の人がいれば、99.9%以上の確率で、誕生日が同じ人がいることになる。これは、直感的には驚くべきことのように思われるのではないか。
いずれにしても、これが「パラドックス」と呼ばれるのは、論理的な矛盾がある、という意味ではなく、あくまでも、一般的な直感に反している、という意味で、このように称されている。
一方で、この数値を100%にするには、当然のことながら、366人(うるう年も考慮すれば、367人)必要ということになる。
これから、わかることは、100%を追求することは極めて難しいということ、わずか0.1%のために5倍以上の人が必要になることになる。似たような例は他でもあると思われる。100%を追求するのはよいことだが、効率性も考慮した対応が、往々にして求められることになる。
同じ考え方により、41人の人がいれば、90%以上の確率で、70人の人がいれば、99.9%以上の確率で、誕生日が同じ人がいることになる。これは、直感的には驚くべきことのように思われるのではないか。
いずれにしても、これが「パラドックス」と呼ばれるのは、論理的な矛盾がある、という意味ではなく、あくまでも、一般的な直感に反している、という意味で、このように称されている。
一方で、この数値を100%にするには、当然のことながら、366人(うるう年も考慮すれば、367人)必要ということになる。
これから、わかることは、100%を追求することは極めて難しいということ、わずか0.1%のために5倍以上の人が必要になることになる。似たような例は他でもあると思われる。100%を追求するのはよいことだが、効率性も考慮した対応が、往々にして求められることになる。
誕生日問題
(2016年09月06日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
| 2025/09/25 | 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年10月21日
今週のレポート・コラムまとめ【10/14-10/20発行分】 -
2025年10月20日
中国の不動産関連統計(25年9月)~販売は前年減が続く -
2025年10月20日
ブルーファイナンスの課題-気候変動より低い関心が普及を阻む -
2025年10月20日
家計消費の動向(単身世帯:~2025年8月)-外食抑制と娯楽維持、単身世帯でも「メリハリ消費」の傾向 -
2025年10月20日
縮小を続ける夫婦の年齢差-平均3歳差は「第二次世界大戦直後」という事実
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか-のレポート Topへ


















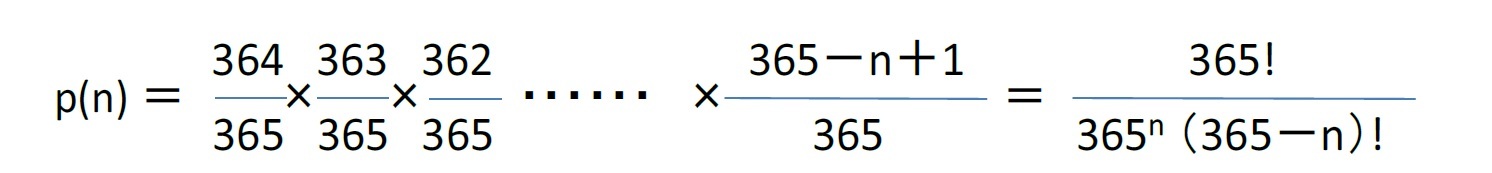
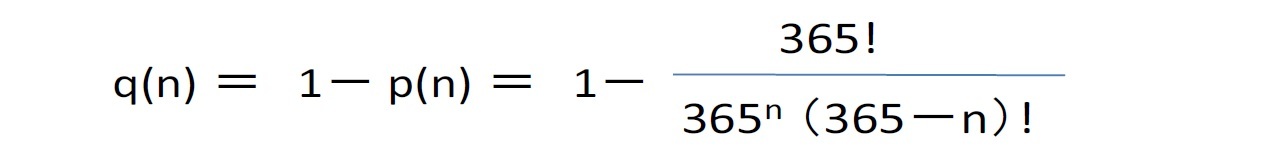
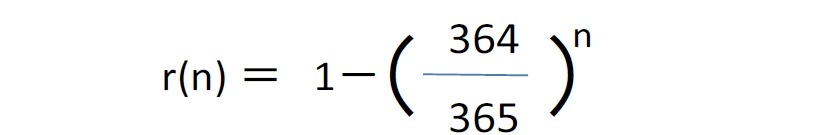

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




