モンティ・ホール問題とベイズ推定－追加情報に応じて取るべき行動をどう変えるか?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

(参考) 一般化したモンティ・ホール問題の命題が成り立つことの説明

以下、命題の成立を説明していく。なお、細部の条件等での厳密さは追求せず、あくまで概要の“説明”にとどめる。その意味で、数学的な“証明”とは異なるものであることをご了承いただきたい。

(一般化したモンティ・ホール問題)
設定:ドアN個(うちアタリW個)、追加情報:司会者はドアn個(うちアタリw個)を開ける
事前確率 W/N　→　事後確率 P

[命題]
(W/N　＋　(N－n－1)×P) / (N－n)　＝　(W－w) / (N－n)
つまり、P　＝　(N－1－N×w/W)/ (N－1－n)　×　W/N

(説明)
解答者は、最初にドア(1)を選択するものとする。

AiやBjなどの事象の記号の意味は、本文のものと同様とする。また、括弧書きは、場合の数を表すものとする。

P(A1) ＝ … ＝ P(AN) ＝ W/N
P(Ai∩…∩Aj)＝1/

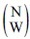　(Ai∩…∩Ajは、W個のA*の「かつ」事象)

P(Bs∩…∩Bt | Ai∩…∩Aj)　(Bs∩…∩Btは、n個のB*の「かつ」事象)について考えてみる。

Ai∩…∩AjのA*の中にA1が含まれている場合、A1∩Ap∩…∩Aqとなり、Ap∩…∩Aqの(W-1)個のA*の添え字と、Bs∩…∩Btのn個のB*の添え字が、ちょうどw個一致しているときに、

P(Bs∩…∩Bt | Ai∩…∩Aj)＝1/{

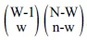}となり、それ以外のときは0となる。

Ai∩…∩AjのA*の中にA1が含まれていない場合、Ai∩…∩AjのW個のA*の添え字と、Bs∩…∩Btのn個のB*の添え字が、ちょうどw個一致しているときに、

P(Bs∩…∩Bt | Ai∩…∩Aj)＝1/{

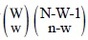}となり、それ以外のときは0となる。

ベイズの定理を使って、P(A1| Bs∩…∩Bt)と、P(Ak| Bs∩…∩Bt) (kは1やB*の添え字以外)を計算して、その比を取りたい。

まず、P(A1| Bs∩…∩Bt)について。

P(A1| Bs∩…∩Bt)＝∑P(A1∩Ap∩…∩Aq| Bs∩…∩Bt) (Ap∩…∩AqのA*の数は(W-1)個)のように、

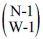個の項の足し算の形に分解できる。さらにベイズの定理を用いて、次のように変形できる。

(ただし、Ap∩…∩Aq 、Au∩…∩Av 、Ai∩…∩AjのA*はA1以外。また、Ap∩…∩Aq とAu∩…∩Avは(W-1)個のA*の「かつ」事象。Ai∩…∩AjはW個のA*の「かつ」事象。)

このうち、P(Bs∩…∩Bt| A1∩Au∩…∩Av)の部分については、Au∩…∩Avの(W-1)個のA*の添え字と、Bs∩…∩Btのn個のB*の添え字がちょうどw個一致している項だけが残り、それ以外は0となって消える。

残る項は、すべて同じ値となるため、1つの項の値に項数を掛け算することで計算できる。0にならない項の数は、次のように表せる。

Bs∩…∩Btのn個のB*の添え字のうち、w個がアタリ(つまり、Au∩…∩AvのA*の添え字と一致)となる必要があり、そのような選び方の場合の数は

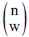通りある。そして、その各場合に、Au∩…∩Avの(W-1)個のA*の添え字のうちBs∩…∩BtのB*の添え字以外のものが、((W-1)-w)個ある。それらは、1以外の添え字全体から、Bs∩…∩Btのn個のB*の添え字を除いた、((N-1)-n)個の中から選ぶことになるので、選び方の場合の数は

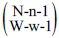通りとなる。この2つの場合の数を掛け算することで、0にならない項数は、

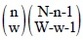と計算できる。

同様に、P(Bs∩…∩Bt| Ai∩…∩Aj)の部分については、0にならない項数は、

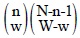となる。

これらを用いることで、P(A1| Bs∩…∩Bt)は、次の通りとなる。

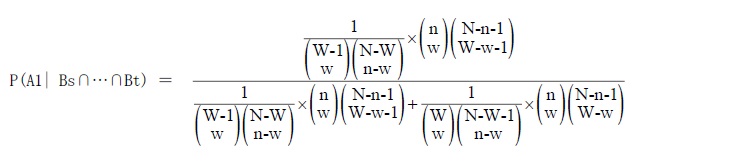
この式は、次のように計算してW/Nに等しいことが確かめられる。

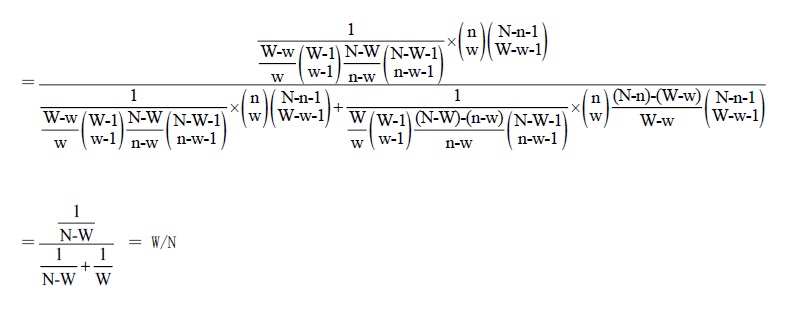次に、P(Ak| Bs∩…∩Bt) (kは1やB*の添え字以外) について。

P(Ak| Bs∩…∩Bt)＝∑P(Ak∩Ap∩…∩Aq| Bs∩…∩Bt) (Ap∩…∩AqのA*の数は(W-1)個)のように、

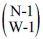個の項の足し算の形に分解できる。さらにベイズの定理を用いて、次のように変形できる。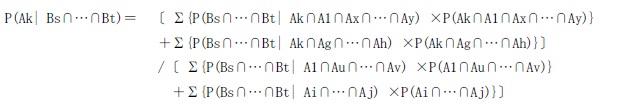

(ただし、Ax∩…∩Ay 、Ag∩…∩Ah のA*はAk、A1以外。Au∩…∩Av 、Ai∩…∩AjのA*はA1以外。また、Ax∩…∩Ayは(W-2)個のA*の「かつ」事象。Ag∩…∩Ah とAu∩…∩Av は(W-1)個のA*の「かつ」事象。Ai∩…∩AjはW個のA*の「かつ」事象。)

このうち、P(Bs∩…∩Bt| Ak∩A1∩Ax∩…∩Ay)の部分については、Ax∩…∩Ayの(W-2)個のA*の添え字と、Bs∩…∩Btのn個のB*の添え字がちょうどw個一致している項だけが残り、それ以外は0となって消える。(その他も同様。)

そこで、次のように計算できる。

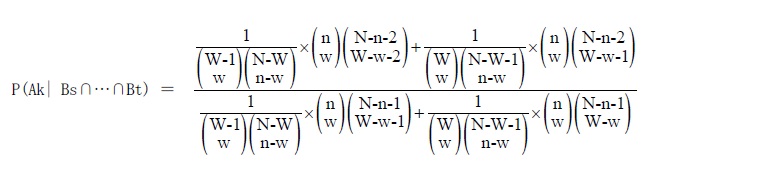
そこで、P(A1| Bs∩…∩Bt)と、P(Ak| Bs∩…∩Bt) (kは1やB*の添え字以外)の比をとる。

この2つの式の分母は同じであるから、分子どうしの比をとればよい。

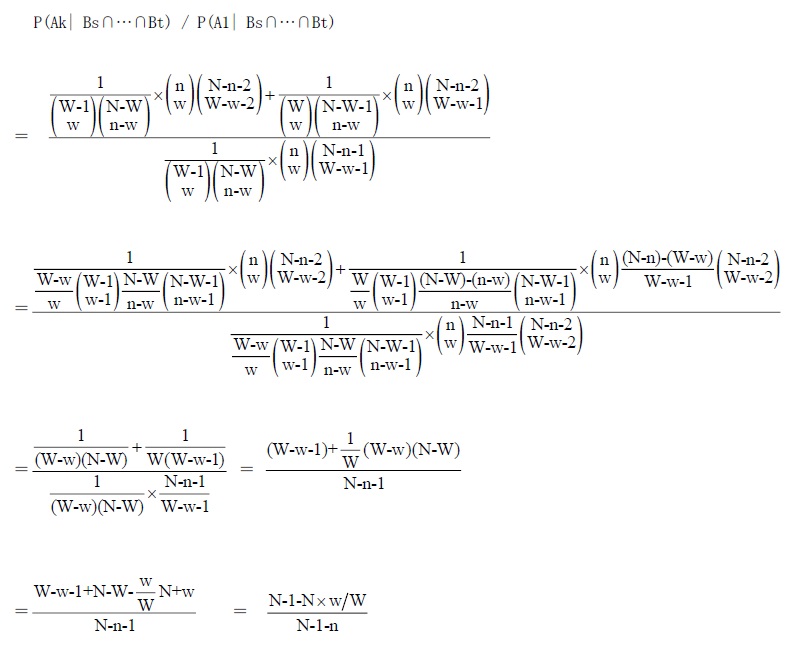
このようにして、命題のPの式の中の、事前確率W/Nに掛け算される分数部分であることが示される。

日付	タイトル	執筆者	媒体
2025/05/27	気候指数 2024年データへの更新－日本の気候の極端さは1971年以降の最高水準を大幅に更新	篠原拓也	基礎研レポート
2025/05/20	「次元の呪い」への対処－モデルの精度を上げるにはどうしたらよいか?	篠原拓也	研究員の眼
2025/05/13	チェス盤を用いた伝心－愛情と計算力があれば心は通じる?	篠原拓也	研究員の眼
2025/05/09	国民負担率 24年度45.8％の見込み－高齢化を背景に、欧州諸国との差は徐々に縮小	篠原拓也	基礎研マンスリー

日付

タイトル

執筆者

媒体

2025/05/27

気候指数 2024年データへの更新－日本の気候の極端さは1971年以降の最高水準を大幅に更新

篠原拓也

基礎研レポート

2025/05/20

「次元の呪い」への対処－モデルの精度を上げるにはどうしたらよいか?

篠原拓也

研究員の眼