- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 曲線にはどんな種類があって、どう社会に役立っているのか(その6)-トロコイド・リマソン・カージオイド等-
コラム
2024年06月06日
文字サイズ
- 小
- 中
- 大
はじめに
学生時代に、複雑な算式を図表で表すと、いろんな形の曲線が描かれるのを勉強したと思う。この時には、「へー、そうなんだ」ぐらいの認識でおられた方も多く、むしろ、こうした算式の取扱いに四苦八苦して、結果として得られている曲線が、社会において、あるいは自然界において、どのような形で現れていて、どう役立っているのか、については、あまり説明がなく、殆ど勉強する機会もなかったのではないかと思われる。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。以前の4回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」及び「クロソイド曲線」について報告した。
前回から、「サイクロイド曲線」等について、複数回に分けて報告することとしている。今回の研究員の眼では、「トロコイド」、「パスカルの蝸牛形」とも呼ばれる「リマソン」及び前回の研究員の眼でも紹介した「カージオイド」等について報告する。
ということで、今回の研究員の眼のシリーズでは、「曲線」について、どんな種類があって、それらが実際の社会における、どのような場面で現れてきて、どう社会に役立っているのかについて、報告している。以前の4回の研究員の眼では、楕円、放物線、双曲線等の「円錐曲線」、「カテナリー曲線」及び「クロソイド曲線」について報告した。
前回から、「サイクロイド曲線」等について、複数回に分けて報告することとしている。今回の研究員の眼では、「トロコイド」、「パスカルの蝸牛形」とも呼ばれる「リマソン」及び前回の研究員の眼でも紹介した「カージオイド」等について報告する。
トロコイド
エピトロコイドとハイポトロコイド
c=bのときが、まさに前回の研究員の眼で示したエピサイクロイド、ハイポサイクロイドとなる。
また、ハイポトロコイドで、a=2b、0<2c<a のとき、楕円となる。楕円はハイポトロコイドの一種ということになる。
また、ハイポトロコイドで、a=2b、0<2c<a のとき、楕円となる。楕円はハイポトロコイドの一種ということになる。
パスカルの蝸牛形(リマソン)
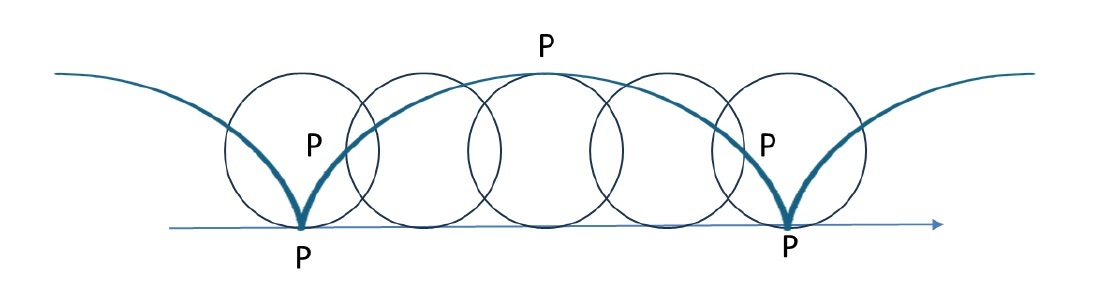
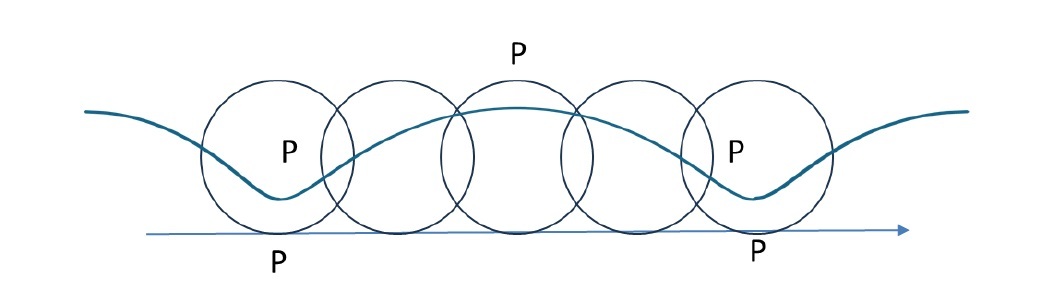
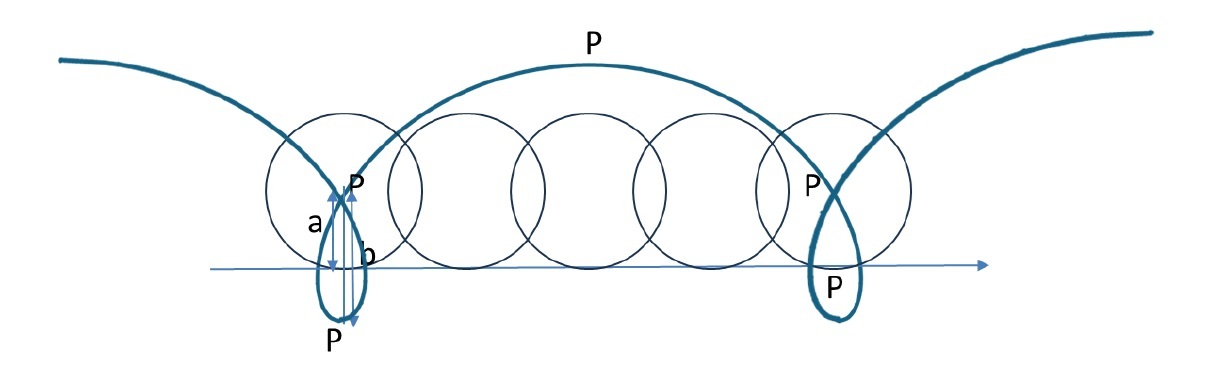
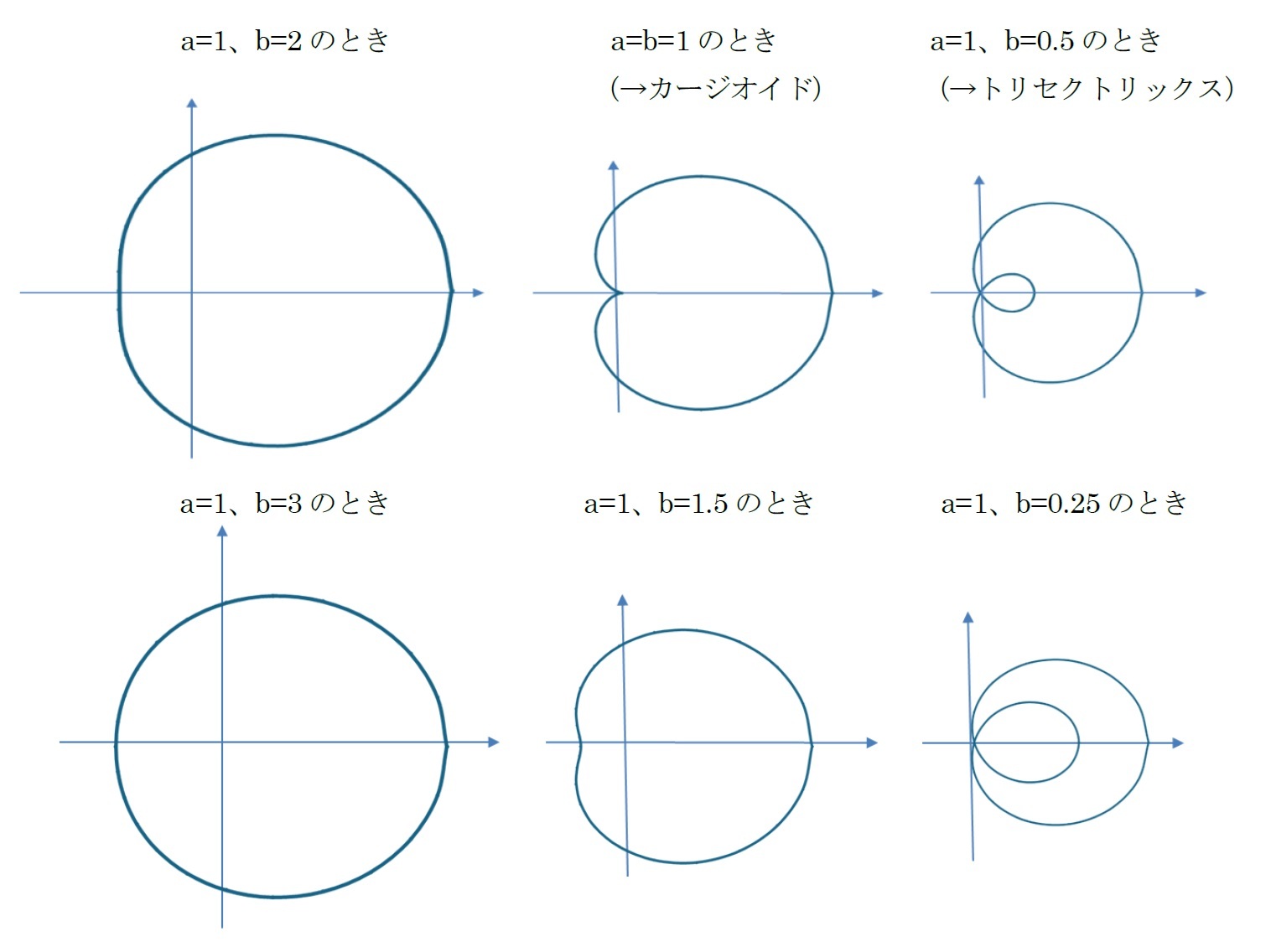
「パスカルの蝸牛形(Limaçon de Pascal)」は、単に「蝸牛線」あるいは「リマソン」と呼ばれている図形で、以下のような図形である。
「リマソン」というのは、フランス語で「蝸牛(かたつむり)」のことであり、ラテン語の「かたつむり」を意味する「limax」に由来しており、まさにその形状から名付けられている。また、ここでの「パスカル」というのは、「人間は考える葦である」などの名文句やパスカルの三角形、定理、原理等で有名な哲学者かつ数学者等であるブレーズ・パスカル(Blaise Pascal)ではなくて、彼の父のエティエンヌ・パスカル(Étienne Pascal)のことを指している。1650年にロバ―ヴァル(Gilles-Personne Roberval)によって、この名が付けられた。なお、リマソンについては、パスカルより前に、有名なドイツの画家であるアルブレヒト・デューラー(Albrecht Dürer)によって発見されており、1525年の「Underweysung der Messung」(測定の仕様)に、リマソンの幾何学的な描き方が述べられているようだ。
「リマソン」は、以下の形で表される1。
「リマソン」というのは、フランス語で「蝸牛(かたつむり)」のことであり、ラテン語の「かたつむり」を意味する「limax」に由来しており、まさにその形状から名付けられている。また、ここでの「パスカル」というのは、「人間は考える葦である」などの名文句やパスカルの三角形、定理、原理等で有名な哲学者かつ数学者等であるブレーズ・パスカル(Blaise Pascal)ではなくて、彼の父のエティエンヌ・パスカル(Étienne Pascal)のことを指している。1650年にロバ―ヴァル(Gilles-Personne Roberval)によって、この名が付けられた。なお、リマソンについては、パスカルより前に、有名なドイツの画家であるアルブレヒト・デューラー(Albrecht Dürer)によって発見されており、1525年の「Underweysung der Messung」(測定の仕様)に、リマソンの幾何学的な描き方が述べられているようだ。
「リマソン」は、以下の形で表される1。
となる。
1 リマソンは、以下のように、いくつかの曲線との関係の中で現れてくる。その中で、aとbの意味合いを示すものとして、例えば、「長さaの線分OAを直径とする円周上に動点Qをとり、直線OQ上に長さbの線分QPとQP´をQの両側にとるとき、点P、P´の描く軌跡」がリマソンとなっている。
(1) P6~P7で述べるように、「円錐曲線の反転図形」になっている。
(2) 円周上の点に対する円の「コンコイド(concoid)」になっている。
点Oと曲線ℓが与えられたとき、曲線ℓ上を点Aが動くとき、直線OA上の点Aから一定の距離にある2点P、Qの軌跡を「曲線ℓのコンコイド」と呼んでいる。曲線ℓが直線の場合として、古代ギリシアの数学者ニコメデスが発見した「ニコメデスのコンコイド」が有名である。
(3) 点(a,0)、半径bの円に対する「垂足曲線(pedal curve)」になっている。なお、定点Oから定曲線Cの各接線に下ろした垂線の足の軌跡をOに対するCの「垂足曲線」と呼んでいる。
(4) 点Pとこれを中心としない円Cがあるとき、中心がC上にありPを通過する円の「包絡線(envelope)」となっている。「包絡線」は与えられた曲線族と接線を共有する曲線である。
これらの曲線については、機会があれば、別途のレポートで報告することとする。
2 以前の研究員の眼「ギリシアの3大作図問題-数学を通じて、ギリシアという国の歴史的位置付けの重みを再認識してみませんか-」(2017.6.19)で述べたように、任意の角度はコンパスと定規のみを使用して三等分することはできない。ただし、(他の手段を用いて構築された)特定の曲線を使用して三等分できる。このような曲線には様々な種類があり、リマソン・トリセクトリックス、マクローリン・トリセクトリックス等が有名である。
1 リマソンは、以下のように、いくつかの曲線との関係の中で現れてくる。その中で、aとbの意味合いを示すものとして、例えば、「長さaの線分OAを直径とする円周上に動点Qをとり、直線OQ上に長さbの線分QPとQP´をQの両側にとるとき、点P、P´の描く軌跡」がリマソンとなっている。
(1) P6~P7で述べるように、「円錐曲線の反転図形」になっている。
(2) 円周上の点に対する円の「コンコイド(concoid)」になっている。
点Oと曲線ℓが与えられたとき、曲線ℓ上を点Aが動くとき、直線OA上の点Aから一定の距離にある2点P、Qの軌跡を「曲線ℓのコンコイド」と呼んでいる。曲線ℓが直線の場合として、古代ギリシアの数学者ニコメデスが発見した「ニコメデスのコンコイド」が有名である。
(3) 点(a,0)、半径bの円に対する「垂足曲線(pedal curve)」になっている。なお、定点Oから定曲線Cの各接線に下ろした垂線の足の軌跡をOに対するCの「垂足曲線」と呼んでいる。
(4) 点Pとこれを中心としない円Cがあるとき、中心がC上にありPを通過する円の「包絡線(envelope)」となっている。「包絡線」は与えられた曲線族と接線を共有する曲線である。
これらの曲線については、機会があれば、別途のレポートで報告することとする。
2 以前の研究員の眼「ギリシアの3大作図問題-数学を通じて、ギリシアという国の歴史的位置付けの重みを再認識してみませんか-」(2017.6.19)で述べたように、任意の角度はコンパスと定規のみを使用して三等分することはできない。ただし、(他の手段を用いて構築された)特定の曲線を使用して三等分できる。このような曲線には様々な種類があり、リマソン・トリセクトリックス、マクローリン・トリセクトリックス等が有名である。
(2024年06月06日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
| 2025/10/02 | IAIGsの指定の公表に関する最近の状況(15)-19の国・地域からの61社に- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年10月31日
交流を広げるだけでは届かない-関係人口・二地域居住に求められる「心の安全・安心」と今後の道筋 -
2025年10月31日
ECB政策理事会-3会合連続となる全会一致の据え置き決定 -
2025年10月31日
2025年7-9月期の実質GDP~前期比▲0.7%(年率▲2.7%)を予測~ -
2025年10月31日
保険型投資商品の特徴を理解すること(欧州)-欧州保険協会の解説文書 -
2025年10月31日
鉱工業生産25年9月-7-9月期の生産は2四半期ぶりの減少も、均してみれば横ばいで推移
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【曲線にはどんな種類があって、どう社会に役立っているのか(その6)-トロコイド・リマソン・カージオイド等-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
曲線にはどんな種類があって、どう社会に役立っているのか(その6)-トロコイド・リマソン・カージオイド等-のレポート Topへ



















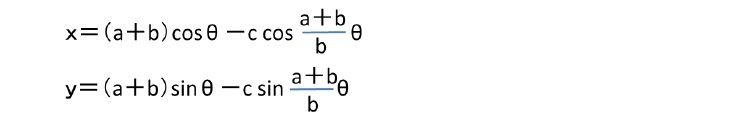
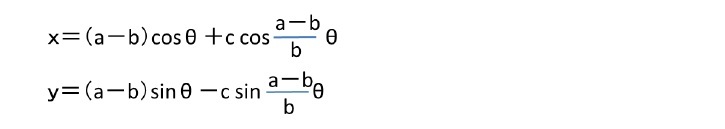
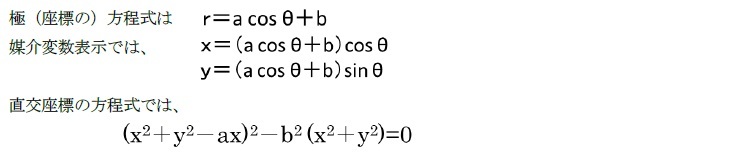
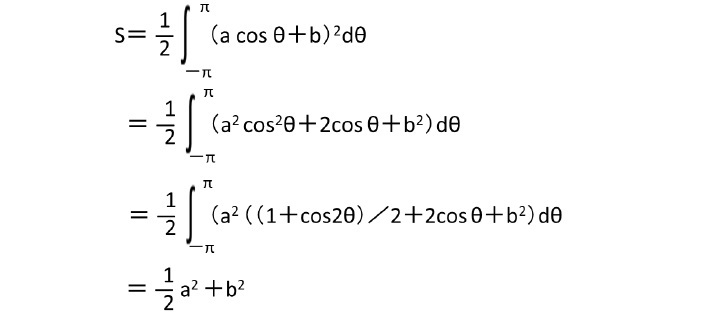


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




