- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが-
NEW
コラム
2025年11月04日
文字サイズ
- 小
- 中
- 大
■要旨
「26」という数字は、アルファベットの文字数として知られているが、それ以外にも宗教との関係で「26」という数字が現れてくるし、「平方数と立方数に挟まれた唯一の自然数」であるという興味深い特徴も有している。
■目次
・はじめに
・英語アルファベットは26文字
・日本二十六聖人
・数字の「26」は平方数と立方数に挟まれた唯一の自然数
・宗教における数字の「26」
・人間の片足の骨は26個と言われている
・散在型有限単純群は26個
・その他の数字の「26」が現れてくる例
・最後に
「26」という数字は、アルファベットの文字数として知られているが、それ以外にも宗教との関係で「26」という数字が現れてくるし、「平方数と立方数に挟まれた唯一の自然数」であるという興味深い特徴も有している。
■目次
・はじめに
・英語アルファベットは26文字
・日本二十六聖人
・数字の「26」は平方数と立方数に挟まれた唯一の自然数
・宗教における数字の「26」
・人間の片足の骨は26個と言われている
・散在型有限単純群は26個
・その他の数字の「26」が現れてくる例
・最後に
はじめに
数字の「26」と聞いて、皆さんは何を思い浮かべるだろうか。「アルファベットが26文字」だということを指摘する人は多いと思われる。ただし、「それ以外には?」と聞かれると答えに窮してしまう人が多いのではないかと思われる。
今回は、この数字の「26」について、それが現れてくる例やその理由等について調べてみた。
今回は、この数字の「26」について、それが現れてくる例やその理由等について調べてみた。
英語アルファベットは26文字
まずは、「アルファベット(alphabet)」の文字数についてである。
「アルファベット」というと、通常は英語のアルファベットを思い浮かべる人が殆どだと思われるが、実はアルファベットにはいろいろな種類がある。我々が通常アルファベットと呼んでいるものは、その中の「ラテンアルファベット(Latin alphabet)」(あるいは「ラテン文字」)と呼ばれているものの中の「英語アルファベット(English alphabet)」のことを指している。「ラテン文字」は、元来、ラテン語の文字であり、古代ラテン人つまり、広義のローマ人が用いたことから「ローマ文字(Roman alphabet)」や「ローマ字」とも呼ばれている。
「アルファベット」というのは、表音文字のうちの音素文字と呼ばれるものの一種で、一つ一つの文字が原則として一つの子音もしくは母音という音素を表すものを指している。ラテンアルファベット以外にも、ギリシャ文字や(ロシア語等の)キリル文字等がある。
さて、この「ラテンアルファベットの基本文字(basic Latin alphabet)」が26文字となっている。「英語アルファベット」はこの基本文字だけで構成されている。これに対して、例えば「ドイツ語アルファベット(German alphabet)」は、ウムラウトと呼ばれるダイアクリティカルマーク(発音区別符号)(上部に付される横並びの2点「¨」)のついた3文字(Ä, Ö, Ü)やエスツェットと称されるリガチャ(合字)(ẞ)を加えた30文字となっている。
「アルファベット」というと、通常は英語のアルファベットを思い浮かべる人が殆どだと思われるが、実はアルファベットにはいろいろな種類がある。我々が通常アルファベットと呼んでいるものは、その中の「ラテンアルファベット(Latin alphabet)」(あるいは「ラテン文字」)と呼ばれているものの中の「英語アルファベット(English alphabet)」のことを指している。「ラテン文字」は、元来、ラテン語の文字であり、古代ラテン人つまり、広義のローマ人が用いたことから「ローマ文字(Roman alphabet)」や「ローマ字」とも呼ばれている。
「アルファベット」というのは、表音文字のうちの音素文字と呼ばれるものの一種で、一つ一つの文字が原則として一つの子音もしくは母音という音素を表すものを指している。ラテンアルファベット以外にも、ギリシャ文字や(ロシア語等の)キリル文字等がある。
さて、この「ラテンアルファベットの基本文字(basic Latin alphabet)」が26文字となっている。「英語アルファベット」はこの基本文字だけで構成されている。これに対して、例えば「ドイツ語アルファベット(German alphabet)」は、ウムラウトと呼ばれるダイアクリティカルマーク(発音区別符号)(上部に付される横並びの2点「¨」)のついた3文字(Ä, Ö, Ü)やエスツェットと称されるリガチャ(合字)(ẞ)を加えた30文字となっている。
日本二十六聖人
「日本二十六聖人」は、1597年2月5日(慶長元年12月19日)豊臣秀吉の命令によって長崎で磔の刑に処された26人のカトリック信者のことを指している。日本でキリスト教の信仰を理由に最高権力者の指令による処刑が行われたのはこれが初めてであった。この出来事を「二十六聖人の殉教」というが、西洋諸国では「聖パウロ三木と仲間たち」とも呼ばれる。26人は後にカトリック教会によって聖人の列に加えられたため、彼らは「日本二十六聖人」と呼ばれることになった。
列聖100年を記念して、長崎の西坂の丘に日本二十六聖人記念館(今井兼次氏の設計)と彫刻家の舟越保武氏による記念碑「昇天のいのり」が建てられた。
列聖100年を記念して、長崎の西坂の丘に日本二十六聖人記念館(今井兼次氏の設計)と彫刻家の舟越保武氏による記念碑「昇天のいのり」が建てられた。
数字の「26」は平方数と立方数に挟まれた唯一の自然数
すると、これは「一意分解環」と呼ばれるものになる。その意味するところは、大雑把に言えば「整数に対する算術の基本定理(素因数分解の一意性)のように(特別の例外を除く)各元が素元(あるいは既約元)3の積に一意に表せる可換環(乗法が可換であるような環)」4となっている。
y3-x2=2 を変形すると√(-2)
y3=(x+√(-2))(x-√(-2))
ここで、(x+√(-2))と(x-√(-2))が 上で互いに素であり、
上で互いに素であり、 は一意分解環であること(これらについては、重要な前提であり、証明が必要だが、ここでは紙面の都合もあり、省略する)から、ある整数aとbを用いて、以下のように表せる。
は一意分解環であること(これらについては、重要な前提であり、証明が必要だが、ここでは紙面の都合もあり、省略する)から、ある整数aとbを用いて、以下のように表せる。
x+√(-2)=(a+b√(-2))3
上式の右辺を展開すると a3-2ab2―4ab2+(3a2b―2b3)√(-2)となることから
3a2b―2b3 =b(3a2―2b2)=1
従って、b=3a2―2b2=±1 となるが、b=-1のときは3a2―2b2=3a2―2>0(a=0とすると、x=√(-2) となってしまうので、a≠0)となることから適さない。よって、b=1、a=±1 となる。
これより、 x+√(-2)=(±1+√(-2))3=±5+ √(-2)
x>0 なので、x=5、よってy=3 となる。
1 ここでは、自然数の定義に「0」を含むか含まないかは気にしない。含まない場合には「正の整数」と言い換えることができる。
2 「初等整数論講義 第2版」高木貞治 共立出版 P305 問題1 の解では、「2次体 のイデアルの類の数が1である」ということを使用して証明している。本稿の以下の証明で省略した証明や「2次体」、「イデアル」、「類」の概念等、詳しい内容については、専門書等を参照していただきたい。
3 単元とその元以外で割り切れない元
4 数学における「環(ring)」とは、台集合(何の構造も持たない、単なる「はだか」の集合)に「加法」(和)及び「乗法」(積)と呼ばれる二種類の二項演算を備えた代数系のこと。
y3-x2=2 を変形すると√(-2)
y3=(x+√(-2))(x-√(-2))
ここで、(x+√(-2))と(x-√(-2))が
 上で互いに素であり、
上で互いに素であり、 は一意分解環であること(これらについては、重要な前提であり、証明が必要だが、ここでは紙面の都合もあり、省略する)から、ある整数aとbを用いて、以下のように表せる。
は一意分解環であること(これらについては、重要な前提であり、証明が必要だが、ここでは紙面の都合もあり、省略する)から、ある整数aとbを用いて、以下のように表せる。x+√(-2)=(a+b√(-2))3
上式の右辺を展開すると a3-2ab2―4ab2+(3a2b―2b3)√(-2)となることから
3a2b―2b3 =b(3a2―2b2)=1
従って、b=3a2―2b2=±1 となるが、b=-1のときは3a2―2b2=3a2―2>0(a=0とすると、x=√(-2) となってしまうので、a≠0)となることから適さない。よって、b=1、a=±1 となる。
これより、 x+√(-2)=(±1+√(-2))3=±5+ √(-2)
x>0 なので、x=5、よってy=3 となる。
1 ここでは、自然数の定義に「0」を含むか含まないかは気にしない。含まない場合には「正の整数」と言い換えることができる。
2 「初等整数論講義 第2版」高木貞治 共立出版 P305 問題1 の解では、「2次体 のイデアルの類の数が1である」ということを使用して証明している。本稿の以下の証明で省略した証明や「2次体」、「イデアル」、「類」の概念等、詳しい内容については、専門書等を参照していただきたい。
3 単元とその元以外で割り切れない元
4 数学における「環(ring)」とは、台集合(何の構造も持たない、単なる「はだか」の集合)に「加法」(和)及び「乗法」(積)と呼ばれる二種類の二項演算を備えた代数系のこと。
宗教における数字の「26」
ユダヤ教において、数字の「26」は「ゲマトリア(gematria)」5という伝統的な数秘術に関連している。ゲマトリアでは、アルファベットの各文字に数値を割り当て、それを使って神聖な意味を解釈している。タナハ(ヘブライ語聖書)で神の名前を表すヘブライ語の四文字 יהוה (アルファベットに置き換えるとYHWH又はJHVH)は、「テトラグラマトン」又は「聖四文字」と呼ばれるが、この四文字をゲマトリア変換した数値の合計は26(YとJは10、Hは5、WとVは6)となっている。したがって、ユダヤ教の神秘的な解釈では、数字の「26」は「神」と解釈されている。
また、ユダヤ教の伝承によると、神は創造以来26代目にトーラー(「指導」、「教え」又は「法律」を意味する)を与えた。トーラーは、ヘブライ語聖書の最初の5冊の本、つまり創世記、出エジプト記、レビ記、民数記、申命記の本をまとめたものである。
5 ゲマトリア(gematria)は、名前、単語又はフレーズを数字として読み取ったり、時には英数字の暗号を使用して数値を代入したりする方法
また、ユダヤ教の伝承によると、神は創造以来26代目にトーラー(「指導」、「教え」又は「法律」を意味する)を与えた。トーラーは、ヘブライ語聖書の最初の5冊の本、つまり創世記、出エジプト記、レビ記、民数記、申命記の本をまとめたものである。
5 ゲマトリア(gematria)は、名前、単語又はフレーズを数字として読み取ったり、時には英数字の暗号を使用して数値を代入したりする方法
人間の片足の骨は26個と言われている
人間の片足の骨は基本的には26個と言われており、以下のような内訳になっている。
 ・趾骨(シコツ)が全部で14個・・・いわゆる足の指
・趾骨(シコツ)が全部で14個・・・いわゆる足の指 基節骨が5個(第一趾から第五趾(親指から小指))
中節骨が4個(第二趾から第五趾(人差し指から小指))
母指(親指)にはない
末節骨が5個(第一趾から第五趾(親指から小指))
・中足骨(チュウソクコツ)が5個・・・足の指の基部
第一中足骨から第五中足骨
・足根骨(ソッコンコツ)が7個・・・踵など、足の後ろ部分
近位足根骨(距骨、踵骨、舟状骨)
遠位足根骨(内側楔状骨、中間楔状骨、外側楔状骨、立方骨)
人間の体の骨は全部で約200個(基本的には206個)あると言われていることから、両足だけで52個の骨があり、身体の骨の4分の1以上は足の部分にあるということになる。それほど足は重要な部位となっている。
なお、28個とする説もあるが、この場合、「種子骨」と呼ばれる親指の中足骨の先端の底面に2つ存在している小さな骨が含められるようだ(上記の図では、この「種子骨」も示されている)。
種子骨については、(1)全ての人に必ず存在するわけではなく、その数や位置には個人差があること、(2)機能的にも、関節や腱の働きを助けるための小さな補助的な骨であり、主要な支持構造としての役割を持つ他の骨とは異なること、(3)解剖学的な標準では、主要な骨格要素に焦点を当てており、種子骨はその位置や機能が個別の骨格要素に統一されていないため、通常は含めないことがより一般的なようだ。
いずれにしても、人間の体には個体差があり、バリエーションも多いとのことである。
散在型有限単純群は26個
「26」は、数学における「散在型有限単純群(Sporadic Finite Simple Groups)」と呼ばれる群6の数となっている。
数学において、「単純群(simple group)」とは、自明でない正規部分群7(それ自身と自明群(単位群 {e}、ただ1つの元からなる群)以外の正規部分群)を持たず、またそれ自身も自明群ではない群である。また、「有限群(finite group)」は、台となる集合が有限個の元しか持たない群である。
「有限単純群(finite simple groups)」については、「有限単純群の分類定理」が存在しており、全ての有限単純群は4つの大まかなクラスに分類される。これらの群は、全ての有限群を構成する基本的な要素となっている(これは素数が整数の基本的な要素となっていることに似ている)。
この定理によると、全ての有限単純群は、以下の群のいずれかと同型8となる(即ち、有限単純群は、(1)(2)(3)の18種類の可算無限族とそのような系統的パターンに従わない26種類の例外で構成される)。
(1) 素数位数の巡回群(Cyclic group of prime order) Cp
(2) 次数5以上の交代群(Alternating Group of degree ≧5) An
(3) 16種類のリー型の単純群(Simple group of Lie type)
ティッツ群(27番目の散在型単純群と見なされることもある)を含む。
(4)26種類の散在型単純群(Sporadic Simple Groups)
そのうちの20種類はモンスター群(最大の散在型単純群)の部分群又は部分商9で、「Happy Family」と呼ばれており、残りの6種類は「pariah」と呼ばれている。このうちの最大のモンスター群の位数(元の数)は、
808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000
= 246·320·59・76・112・133・17・19・23・29・31・41・47・59・71 ≈ 8×1053
となっている。
6 数学における「群(group)」とは、ある二項演算とその対象となる集合とを合わせて見たときに結合性を伴い単位元と逆元を備えるものをいう。数学において最も基本的と見なされる代数的構造の一つであり、数学や物理学全般において、さまざまな構成に対する基礎的な枠組みを与えている。
7 群Gの部分群Nが「正規部分群(normal subgroup)」であるとは、Nの任意の元nとGの任意の元gに対して、元 gng−1 が再びNに属するときにいう。
8 2つの群が「同型(isomorphic)」であるとは、2つの群の間の関数であって与えられた群演算と両立する方法で群の元の間の一対一対応ができることをいう。
9 「部分群(subgroup)」がある群Gの部分集合で同じ演算の下で群の条件(結合法則、単位元の存在、逆元の存在)を満たすものであるのに対して、「部分商(quotient group)」は群Gの正規部分群Nを使って構成され、大きい群の要素を同一視できる関係により一塊としてみなすことで得られる群で、それぞれの塊がその群の元となる。
数学において、「単純群(simple group)」とは、自明でない正規部分群7(それ自身と自明群(単位群 {e}、ただ1つの元からなる群)以外の正規部分群)を持たず、またそれ自身も自明群ではない群である。また、「有限群(finite group)」は、台となる集合が有限個の元しか持たない群である。
「有限単純群(finite simple groups)」については、「有限単純群の分類定理」が存在しており、全ての有限単純群は4つの大まかなクラスに分類される。これらの群は、全ての有限群を構成する基本的な要素となっている(これは素数が整数の基本的な要素となっていることに似ている)。
この定理によると、全ての有限単純群は、以下の群のいずれかと同型8となる(即ち、有限単純群は、(1)(2)(3)の18種類の可算無限族とそのような系統的パターンに従わない26種類の例外で構成される)。
(1) 素数位数の巡回群(Cyclic group of prime order) Cp
(2) 次数5以上の交代群(Alternating Group of degree ≧5) An
(3) 16種類のリー型の単純群(Simple group of Lie type)
ティッツ群(27番目の散在型単純群と見なされることもある)を含む。
(4)26種類の散在型単純群(Sporadic Simple Groups)
そのうちの20種類はモンスター群(最大の散在型単純群)の部分群又は部分商9で、「Happy Family」と呼ばれており、残りの6種類は「pariah」と呼ばれている。このうちの最大のモンスター群の位数(元の数)は、
808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000
= 246·320·59・76・112・133・17・19・23・29・31・41・47・59・71 ≈ 8×1053
となっている。
6 数学における「群(group)」とは、ある二項演算とその対象となる集合とを合わせて見たときに結合性を伴い単位元と逆元を備えるものをいう。数学において最も基本的と見なされる代数的構造の一つであり、数学や物理学全般において、さまざまな構成に対する基礎的な枠組みを与えている。
7 群Gの部分群Nが「正規部分群(normal subgroup)」であるとは、Nの任意の元nとGの任意の元gに対して、元 gng−1 が再びNに属するときにいう。
8 2つの群が「同型(isomorphic)」であるとは、2つの群の間の関数であって与えられた群演算と両立する方法で群の元の間の一対一対応ができることをいう。
9 「部分群(subgroup)」がある群Gの部分集合で同じ演算の下で群の条件(結合法則、単位元の存在、逆元の存在)を満たすものであるのに対して、「部分商(quotient group)」は群Gの正規部分群Nを使って構成され、大きい群の要素を同一視できる関係により一塊としてみなすことで得られる群で、それぞれの塊がその群の元となる。
その他の数字の「26」が現れてくる例
・3乗した数の各桁の数の和が元の数になる数である。263 = 17576, 1 + 7 + 5 + 7 + 6 = 26
このような数は6個しかなく、他は1, 8, 17, 18, 27
・東京都にある市の数は26
・スイスの州の数は26
このような数は6個しかなく、他は1, 8, 17, 18, 27
・東京都にある市の数は26
・スイスの州の数は26
最後に
今回は数字の「26」について、それが現れてくる例やその理由等について、報告してきた。
「26」という数字なんて、アルファベットの文字数以外に現れてくる例は何もないだろう、と思われていた方も多いかもしれない。しかし、調べてみると、結構面白い例が発見できたのではないかと思われる。特に、個人的には、「数字の「26」は平方数と立方数に挟まれた唯一の自然数である」という事実に大変好奇心をくすぐられた。
結局のところ、どんな数字も思わぬところで現れてきて、それなりに意味ある存在感を示しているということなのかもしれない。
「26」という数字なんて、アルファベットの文字数以外に現れてくる例は何もないだろう、と思われていた方も多いかもしれない。しかし、調べてみると、結構面白い例が発見できたのではないかと思われる。特に、個人的には、「数字の「26」は平方数と立方数に挟まれた唯一の自然数である」という事実に大変好奇心をくすぐられた。
結局のところ、どんな数字も思わぬところで現れてきて、それなりに意味ある存在感を示しているということなのかもしれない。
(2025年11月04日「研究員の眼」)
関連レポート
- 数字の「49」に関わる各種の話題-49という数字に皆さんはどんなイメージを有しているのだろう-
- 数字の「48」に関わる各種の話題-48という数字は、結構いろいろな場面で現れてくるようだ-
- 数字の「36」に関わる各種の話題-36という数字は、実は意外なところでも現れてくるようだ-
- 数字の「100」に関わる各種の話題-「100」は極めて多くの場面で現れるが-
- 数字の「3」に関わる各種の話題-数多くの場面で現れてくる数字だが-
- 数字の「60」に関わる各種の話題-時間の基礎となる数字なので馴染み深い数字だと思われるが-
- 数字の「10」に関わる各種の話題-十進法を採用している現代社会では、「10」という数字は特別な意味を有している-
- 数字の「101」に関わる各種の話題-「101」と聞いて、多くの皆さんが思い浮かべるのは-
- 数字の「1260」と「1729」について-これらの数字にどんな意味があるのだろう-
- 数字の「108」に関わる各種の話題-「108」と言えば、除夜の鐘が撞かれる回数だが-
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月04日
数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- -
2025年11月04日
ユーロ圏消費者物価(25年10月)-2%目標に沿った推移が継続 -
2025年11月04日
米国個人年金販売額は2025年上半期も過去最高記録を更新-但し保有残高純増は別の課題- -
2025年11月04日
パワーカップル世帯の動向(2)家庭と働き方~DINKS・子育て・ポスト子育て、制度と夫婦協働が支える -
2025年11月04日
「ブルー寄付」という選択肢-個人の寄付が果たす、資金流入の突破口
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが-のレポート Topへ


















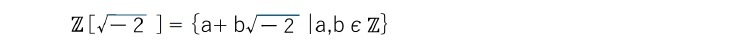

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




