NEW
コラム
2025年08月07日

複素数について（その３）－複素数の工学・物理学への応用－

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする

文字サイズ

  • 小
  • 中
  • 大
全文ダウンロード（PDF）

虚数時間（虚時間）

「虚数時間又は虚時間（imaginary time）」というのは、虚の時間、つまり、単位時間の虚数（純虚数）倍で表される時間である。と言われても、何のことかよくわからない、というのが正直なところだろう。

英国の理論物理学者であるスティーヴン・ホーキング（Stephen Hawking）は、1965年に一般相対性理論12が破綻する特異点の存在を証明した「特異点定理」を（2020年のノーベル物理学賞受賞者でもある）ロジャー・ペンローズ（Roger Penrose）と共に発表し、さらに1974年には、「ホーキング放射」と呼ばれるブラックホールが放出する放射線の存在に関する理論的予測を発表して、量子宇宙論という分野を形作った。ホーキング博士は、一般相対性理論と量子力学を結びつけた量子重力論を提示し、一般相対性理論を破綻させることなく、宇宙の始まりを説明することに成功している。

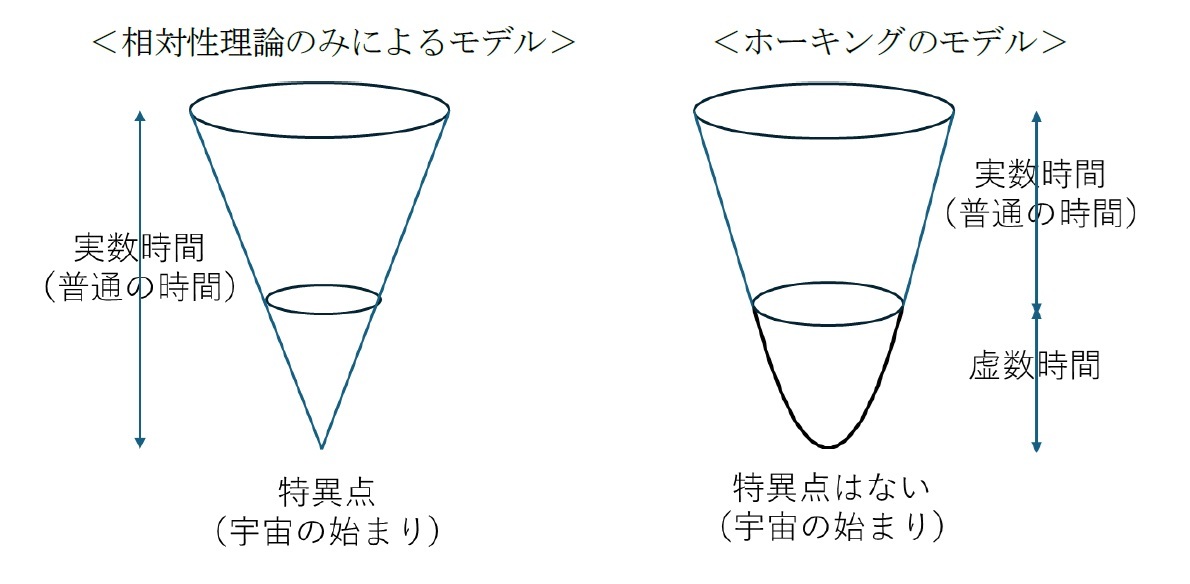
ジェームス・ハートル（James Hartle）とスティーヴン・ホーキングによる「無境界仮説」に基づけば、宇宙の始まりには、「普通の時間（実数時間）」ではなく、「虚数時間」が流れていたとし、このように考えることで、時間と空間の区別がなくなり、厄介な存在である特異点を取り除くことができることになる。

虚数の時間は数学的にいうと「空間の一方向」だと考えられる。通常の、縦、横、高さに加えての第4の方向が「虚数時間」となる。宇宙誕生の時、時間はなく、空間の4方向が存在していたが、その空間のうちの1つの方向が変質し実数の時間になったと考える。
＜相対性理論のみによるモデル＞/＜ホーキングのモデル＞
ホーキング博士は、虚数の時間が実数に変化した時が「トンネル効果」13のトンネルを出た瞬間にあたり、宇宙が誕生することになり、さらに実数時間の流れとともに、宇宙は急速に膨張を始めて、現在の宇宙になったと考えた。
 
12 時間や空間（時空間）と慣性力に基づく考察から、時空間の観測や重力を体系的に論じた物理理論。
13 量子力学において、波動関数がポテンシャル障壁を超えて伝播する現象。

光の屈折と吸収

学生時代に、光の屈折を学んだことを覚えておられる方も多いと思われる。光がガラスや水等の物質（媒質）に斜め方向から入ってくると、光はそのまま直進するではなくて、境界において曲がる。これを光の「屈折」といい、光が曲がる度合いが「屈折率」となる。

屈折率は、「物質中の光速÷真空中の光速」として定義され、物質によって決まっており、物質中での光の進み方を記述する上での指標となっている。２つの物質（例えば、空気と水）の屈折率の差が大きいほど、光は大きく曲がることになる。また、物質によっては光を「吸収」することもある。

こうした光の屈折や吸収の事象を表現するのに、虚数が使用される。

具体的には、

複素屈折率＝通常の屈折率－i×減衰係数

と表すことによって、実部は通常の屈折率、虚部は媒質固有のもので、屈折と同時に起こる吸収の効果を表すことができる。

複素屈折率が虚部を有しない場合、それは通常の屈折率となる。

これに対して、複素屈折率が虚部を有すると、光の一部が吸収されて、「減衰」（光の強さが弱まること）が発生することになる。

実部は、光の速さ（波長）に関係し、これが大きいほど速さが小さくなり、波長が短くなる。一方で、虚部は、光の減衰に関係し、これが大きいほど減衰が大きくなる。

このように、虚数を使用することで、光の「速さ」と「減衰」という２つの要素を有する現象を１つの式で表すことができることになる。

最後に

虚数及び複素数を巡る話題について、複数回に分けて報告することにしているが、今回は、複素数が工学や物理学の世界において、どのように有効に利用されているのかということで、電気・電子工学や量子力学等に関するトピックについて簡単に紹介した。

私の能力不足から、十分に容易な説明ができなかったが、それでも複素数の存在が科学技術の進展に大きく貢献してきているということを若干でもご認識いただけたのではないかと思っている。

次回は、虚数や複素数が数学の世界でどのように利用されているのかについて、前回の研究員の眼で紹介した方程式以外のトピックについて報告する。

« 1 2

本資料記載のデータは各種の情報源から入手・加工したものであり、その正確性と完全性を保証するものではありません。
また、本資料は情報提供が目的であり、記載の意見や予測は、いかなる契約の締結や解約を勧誘するものではありません。

(2025年08月07日「研究員の眼」)

このレポートの関連カテゴリ

Xでシェアする Facebookでシェアする
全文ダウンロード（PDF）

中村 亮一

レポートについてお問い合わせ
(取材・講演依頼)

週間アクセスランキング

保険 総合 領域別

    更新もっと見る

    更新もっと見る

    ピックアップ

    レポート紹介

    お知らせ

    お知らせ一覧

    【複素数について（その３）－複素数の工学・物理学への応用－】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。

    複素数について（その３）－複素数の工学・物理学への応用－のレポート　Topへ