- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 小数について(その3)-非循環小数を巡る話題-
コラム
2023年03月01日
文字サイズ
- 小
- 中
- 大
この数は、上記のように、小数点以下の自然数nの階乗n!の桁(1!=1桁目、2!=2桁目、3!=6桁目、4!=24桁目、・・・)の数が1、その他は0となる数である。その定義から、この数は明らかに正規数ではない。この数は、1844年に、フランスの数学者であるジョゼフ・リウヴィル(Joseph Liouville)(1809-1882)によって、超越数であることが証明された初めての数である。その意味で、これは無理数で(代数的数ではない)超越数の非正規数の例となっており、超越数といえども正規数と限らないことを示している。
なお、「リウヴィル数」は、以下の条件を満たす実数αのことをいう。
任意の正の整数 n に対して、
なお、「リウヴィル数」は、以下の条件を満たす実数αのことをいう。
任意の正の整数 n に対して、
を満たす有理数p/q(q>1)が少なくとも1つ存在する。
リウヴィル数は超越数である(リウヴィルの定理)。0 でない任意の実数は、2つのリウヴィル数の和及び積で表現できる、とされている。
リウヴィル数は超越数である(リウヴィルの定理)。0 でない任意の実数は、2つのリウヴィル数の和及び積で表現できる、とされている。
円周率πについて
先に述べたように、πが正規数であるかどうかについては未解決問題となっている。
2022年6月にGoogleは、πを小数点以下100兆桁まで計算したことを発表しているが5、この限りにおいては 0 から 9 までの数字がランダムに現れているように見えている。ただし、それが乱数列であるのか、また、πが正規数であるのか、は分かっていない。0 から 9 が均等に現れるのかどうかだけでなく、それらが無数に現れるのかどうかも分かっていない。
なお、πが正規数であることが証明され、「πにはあらゆる有限数列が含まれている」ということになれば、どなたであれ、その方の誕生日(例えば、1953年6月12日ならば「19530612 」という8桁の数字列)がπの中に現れる確率は1/108となり、携帯電話番号(例えば、090‐1234‐5678ならば「09012345678」という11桁の数字列)がπの中に現れる確率は1/1011となる。
5 因みに、100兆桁目の数字は「0」だったとされている。
2022年6月にGoogleは、πを小数点以下100兆桁まで計算したことを発表しているが5、この限りにおいては 0 から 9 までの数字がランダムに現れているように見えている。ただし、それが乱数列であるのか、また、πが正規数であるのか、は分かっていない。0 から 9 が均等に現れるのかどうかだけでなく、それらが無数に現れるのかどうかも分かっていない。
なお、πが正規数であることが証明され、「πにはあらゆる有限数列が含まれている」ということになれば、どなたであれ、その方の誕生日(例えば、1953年6月12日ならば「19530612 」という8桁の数字列)がπの中に現れる確率は1/108となり、携帯電話番号(例えば、090‐1234‐5678ならば「09012345678」という11桁の数字列)がπの中に現れる確率は1/1011となる。
5 因みに、100兆桁目の数字は「0」だったとされている。
円周率πの中に見られる不思議な数列
因みに、十進法で表記した時のπの値の中には、不思議な数列が数多く発見されている。例えば、以下のものが挙げられる(いずれも初めて現れるケースを例示)。
(1) ファインマン・ポイント(Feynman point)
小数点以下762桁目から始まる6個の「9」の並びのことをいい、朝永振一郎氏とともにノーベル物理学賞を共同受賞した、米国の物理学者リチャード・ファインマン(Richard Feynman)(1918-1988)が、円周率をこの桁まで暗記したいと講義の中で述べたことから名付けられたとされているが、その真偽のほどは明らかではないようだ。
次に同じ数字が連続して6個並ぶのは、193,034桁目から始まる「9」で、その次は、222,299桁目から始まる「8」である。ほかの数字では「0」の並びが最も遅く現れ、1,699,927桁目からとなっている。
(2) 同じ数字が連続する並び
小数点以下2兆1641億6466万9332桁目から、「8」が13桁
小数点以下3682億9989万8266桁目から、「7」が12桁
小数点以下8978億3131万6566桁目から、「9」が12桁
小数点以下1兆410億3260万9981桁目から、「1」が12桁
等々
(3) 自然数が順に並ぶ数列
小数点以下173億8759万4880桁目から、「0123456789」
小数点以下532億1768万1704桁目から、「01234567890」
小数点以下423億2175万8803桁目から、「0987654321」
(4) 314159265358(円周率の初めの12桁の数字)
小数点以下1兆1429億531万8634桁目から、12桁
なお、最初の6桁(314159)に限れば、1000万桁までに6回現れる。
(1) ファインマン・ポイント(Feynman point)
小数点以下762桁目から始まる6個の「9」の並びのことをいい、朝永振一郎氏とともにノーベル物理学賞を共同受賞した、米国の物理学者リチャード・ファインマン(Richard Feynman)(1918-1988)が、円周率をこの桁まで暗記したいと講義の中で述べたことから名付けられたとされているが、その真偽のほどは明らかではないようだ。
次に同じ数字が連続して6個並ぶのは、193,034桁目から始まる「9」で、その次は、222,299桁目から始まる「8」である。ほかの数字では「0」の並びが最も遅く現れ、1,699,927桁目からとなっている。
(2) 同じ数字が連続する並び
小数点以下2兆1641億6466万9332桁目から、「8」が13桁
小数点以下3682億9989万8266桁目から、「7」が12桁
小数点以下8978億3131万6566桁目から、「9」が12桁
小数点以下1兆410億3260万9981桁目から、「1」が12桁
等々
(3) 自然数が順に並ぶ数列
小数点以下173億8759万4880桁目から、「0123456789」
小数点以下532億1768万1704桁目から、「01234567890」
小数点以下423億2175万8803桁目から、「0987654321」
(4) 314159265358(円周率の初めの12桁の数字)
小数点以下1兆1429億531万8634桁目から、12桁
なお、最初の6桁(314159)に限れば、1000万桁までに6回現れる。
(参考)乱数列
「乱数列」というのは、まさにランダムな数列のことを意味しており、現在得られている数列から次の数が予測できない数列、のことを指している。
乱数列の種類には、「一様乱数」(ある有限の区間を区切って、その区間内で全ての実数が同じ確率で現れるような連続一様分布に従う乱数)や「正規乱数」(正規分布に従う乱数)等がある。
正規数でなければ、その数列は乱数列でないことになる。
乱数列の種類には、「一様乱数」(ある有限の区間を区切って、その区間内で全ての実数が同じ確率で現れるような連続一様分布に従う乱数)や「正規乱数」(正規分布に従う乱数)等がある。
正規数でなければ、その数列は乱数列でないことになる。
最後に
今回は、小数を巡る話題のうち、「非循環小数」を巡る話題について報告した。
非循環小数とは無理数のことだが、これを小数という観点から捉えると、また興味深い話題があることがご認識いただけたのではないかと思っている。
次回は、小数が日常生活や社会においてどのように使われているのか、について述べることとする。
非循環小数とは無理数のことだが、これを小数という観点から捉えると、また興味深い話題があることがご認識いただけたのではないかと思っている。
次回は、小数が日常生活や社会においてどのように使われているのか、について述べることとする。
(2023年03月01日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/13 | 数字の「27」に関わる各種の話題-27は3の3乗だが- | 中村 亮一 | 研究員の眼 |
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
新着記事
-
2025年11月18日
今週のレポート・コラムまとめ【11/11-11/17発行分】 -
2025年11月17日
タイGDP(25年7-9月期)~外需の鈍化と観光の伸び悩みで景気減速 -
2025年11月17日
【令和時代の2人の姿】入籍月の変化にみる「イマドキの選択」とは -
2025年11月17日
QE速報:2025年7-9月期の実質GDPは前期比▲0.4%(年率▲1.8%)-トランプ関税の影響が顕在化し、6四半期ぶりのマイナス成長 -
2025年11月14日
マレーシアGDP(2025年7-9月期)~内需は底堅く、外需は純輸出が改善
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【小数について(その3)-非循環小数を巡る話題-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
小数について(その3)-非循環小数を巡る話題-のレポート Topへ


















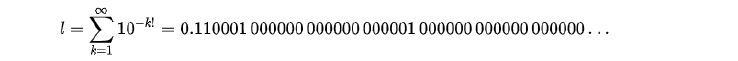


 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




