- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 白銀比τ等について-白銀比とはどのようなもので、どんな場面で使用されているのか-
コラム
2020年12月14日
文字サイズ
- 小
- 中
- 大
はじめに
前回と前々回の研究員の眼では、「黄金比」について紹介した。「黄金比」は実は「貴金属比」と呼ばれているものの1つである。今回は、その他の代表的な貴金属比である「白銀比」等について紹介する。
「黄金比」が「安定した美感を与え」、「調和の取れた美しさがある」ことから、特に西洋人の間で好まれているということを述べたが、日本においては、今回述べる「白銀比」の方が馴染みやすく、人気があるとの意見がある。ただし、「黄金比」に比べて、「白銀比」については、建築やデザインの分野で活躍されている方々を除くと、あまり知られていないと思われる。
今回は、この「白銀比」を中心に触れてみる。なお、「白銀比」と呼ばれるものには、2つの定義があるが、まずは貴金属比の1つとしての定義を説明し、その後より一般的に使用されている定義を説明する。
「黄金比」が「安定した美感を与え」、「調和の取れた美しさがある」ことから、特に西洋人の間で好まれているということを述べたが、日本においては、今回述べる「白銀比」の方が馴染みやすく、人気があるとの意見がある。ただし、「黄金比」に比べて、「白銀比」については、建築やデザインの分野で活躍されている方々を除くと、あまり知られていないと思われる。
今回は、この「白銀比」を中心に触れてみる。なお、「白銀比」と呼ばれるものには、2つの定義があるが、まずは貴金属比の1つとしての定義を説明し、その後より一般的に使用されている定義を説明する。
貴金属比とは
黄金比は、いわゆる「貴金属比(metallic ratio)」と呼ばれるものの1つである。
「第n貴金属比」とは、

で表される比のことである。
線分比 a : b が第n貴金属比であるとは、
( b − n a ) : a = a : b
が成り立つことを意味する。

を「第n貴金属数(metallic number)」という。
第n貴金属数は、二次方程式 x2 − nx − 1 = 0 の正の解となる。
この一般的な定義の中で、n=1 の場合が、「黄金比」に相当することになる。また、n=2 の場合が、「白銀比(silver ratio)」と呼ばれ、n=3 の場合が、「青銅比(bronze ratio)」と呼ばれることになる。
「第n貴金属比」とは、

で表される比のことである。
線分比 a : b が第n貴金属比であるとは、
( b − n a ) : a = a : b
が成り立つことを意味する。

を「第n貴金属数(metallic number)」という。
第n貴金属数は、二次方程式 x2 − nx − 1 = 0 の正の解となる。
この一般的な定義の中で、n=1 の場合が、「黄金比」に相当することになる。また、n=2 の場合が、「白銀比(silver ratio)」と呼ばれ、n=3 の場合が、「青銅比(bronze ratio)」と呼ばれることになる。
「第2貴金属比」としての白銀比とは
改めて、「白銀比(silver ratio)」というのは、通常ギリシア文字の「τ(タウ)」という記号で表される「白銀数」を用いて表現される比率、のことで、「白銀数(silver number)」は、
 という数字になる。白銀数も、黄金数と同様に無理数である。
という数字になる。白銀数も、黄金数と同様に無理数である。
「白銀比」は、この黄金数を用いて、
 と表されることになる。
と表されることになる。
この白銀比を「連分数」と呼ばれるもので表示すると、以下のように表示される。

また、三角関数を用いると以下のように表示される。

 という数字になる。白銀数も、黄金数と同様に無理数である。
という数字になる。白銀数も、黄金数と同様に無理数である。「白銀比」は、この黄金数を用いて、
 と表されることになる。
と表されることになる。この白銀比を「連分数」と呼ばれるもので表示すると、以下のように表示される。

また、三角関数を用いると以下のように表示される。

「第2貴金属比」としての白銀比の使用例等
「大和比」と呼ばれる白銀比とは
白銀比の意味するところ
白銀比の意味するところについては、その定義で述べた通りであるので、ここでは繰り返さない。
縦横比(縦と横の辺の長さの比)が白銀比の長方形を「白銀長方形(silver rectangle)」というが、2つの白銀比に対応して、それぞれ や
や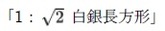 (あるいは単に
(あるいは単に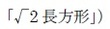 と呼んだりする。両者には、以下の関係がある。
と呼んだりする。両者には、以下の関係がある。
(1)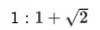 白銀長方形からもっとも大きい正方形を取り去ると、
白銀長方形からもっとも大きい正方形を取り去ると、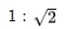 白銀長方形となる。
白銀長方形となる。
(2)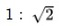 白銀長方形からもっとも大きい正方形を取り去ると、
白銀長方形からもっとも大きい正方形を取り去ると、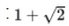 白銀長方形となる。
白銀長方形となる。
また、
(3)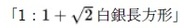 から最大正方形を(1つではなくて)2つ切り落とした残りの長方形は、やはり
から最大正方形を(1つではなくて)2つ切り落とした残りの長方形は、やはり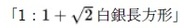 となり、もとの長方形の相似になる。
となり、もとの長方形の相似になる。
(4)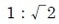 白銀長方形を長辺で2分すると、それぞれが
白銀長方形を長辺で2分すると、それぞれが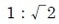 白銀長方形となる。 このうち、(1)はその定義から明らかであり、(2)が証明されれば、(3)も証明される。
白銀長方形となる。 このうち、(1)はその定義から明らかであり、(2)が証明されれば、(3)も証明される。
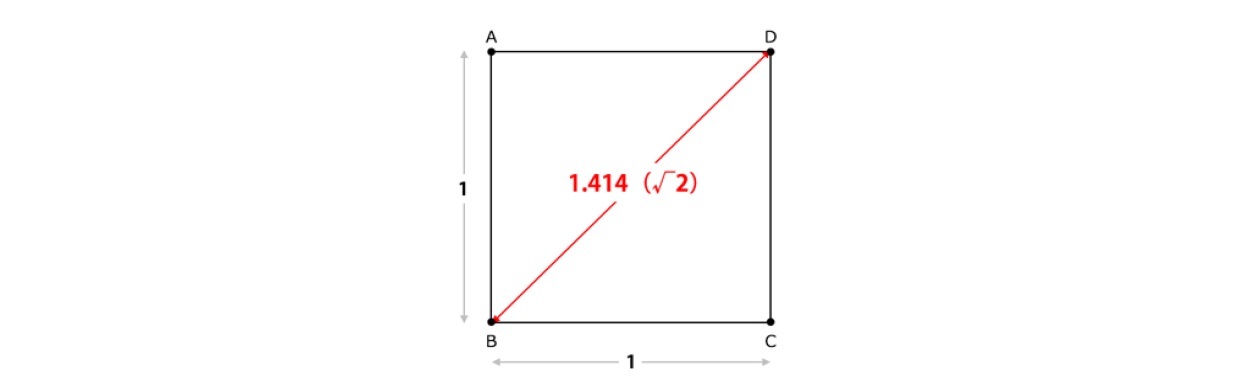
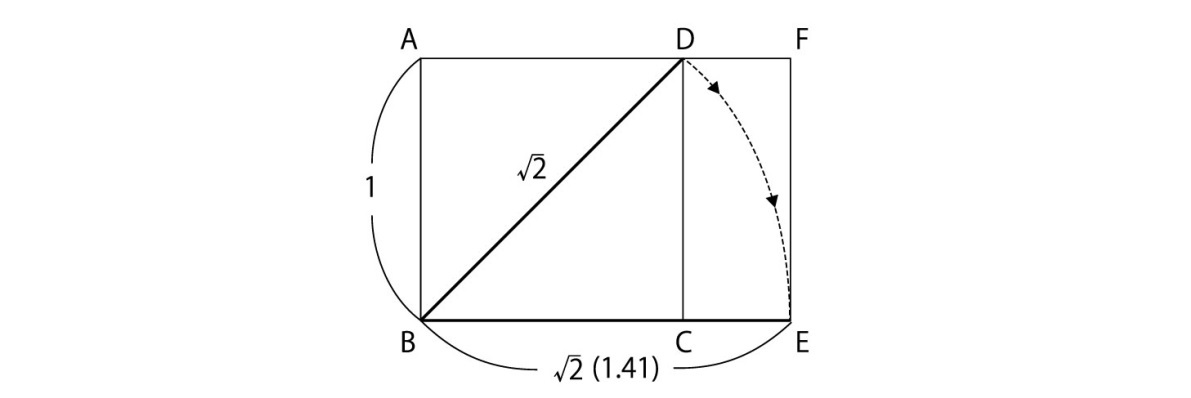
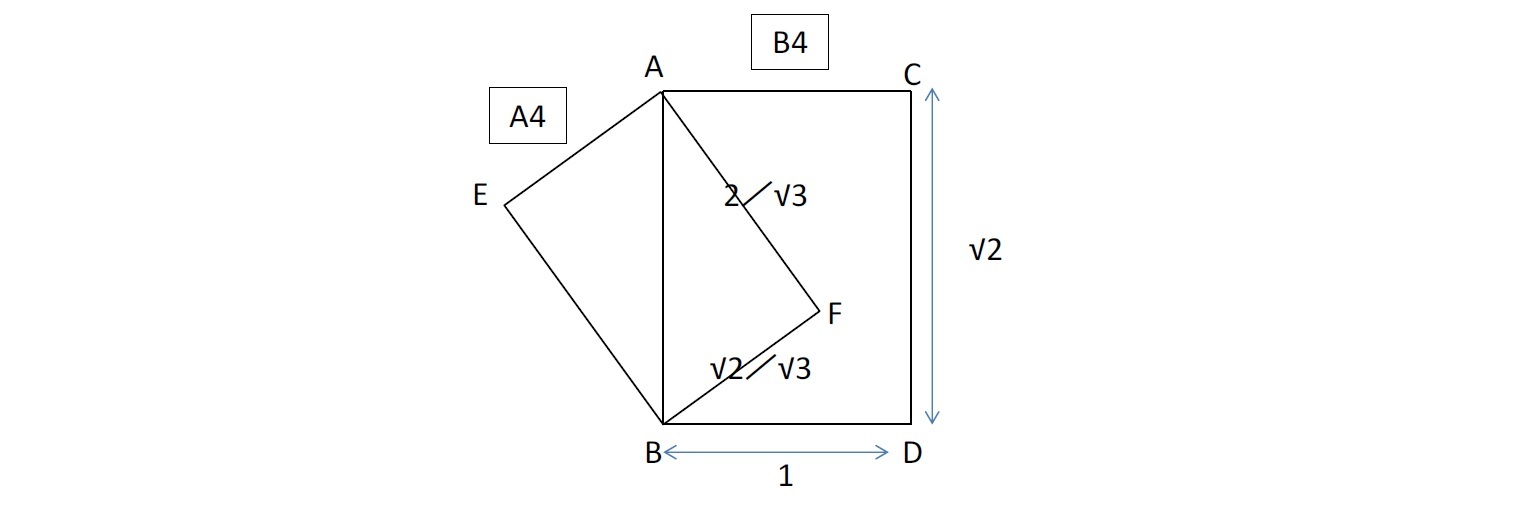
(2)については、下記のような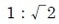 白銀長方形の図において、CEとEFの比率が、
白銀長方形の図において、CEとEFの比率が、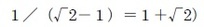 となることから証明される。
となることから証明される。
縦横比(縦と横の辺の長さの比)が白銀比の長方形を「白銀長方形(silver rectangle)」というが、2つの白銀比に対応して、それぞれ
 や
や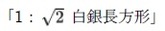 (あるいは単に
(あるいは単に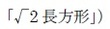 と呼んだりする。両者には、以下の関係がある。
と呼んだりする。両者には、以下の関係がある。(1)
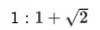 白銀長方形からもっとも大きい正方形を取り去ると、
白銀長方形からもっとも大きい正方形を取り去ると、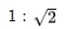 白銀長方形となる。
白銀長方形となる。(2)
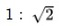 白銀長方形からもっとも大きい正方形を取り去ると、
白銀長方形からもっとも大きい正方形を取り去ると、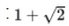 白銀長方形となる。
白銀長方形となる。また、
(3)
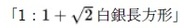 から最大正方形を(1つではなくて)2つ切り落とした残りの長方形は、やはり
から最大正方形を(1つではなくて)2つ切り落とした残りの長方形は、やはり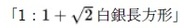 となり、もとの長方形の相似になる。
となり、もとの長方形の相似になる。(4)
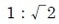 白銀長方形を長辺で2分すると、それぞれが
白銀長方形を長辺で2分すると、それぞれが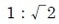 白銀長方形となる。 このうち、(1)はその定義から明らかであり、(2)が証明されれば、(3)も証明される。
白銀長方形となる。 このうち、(1)はその定義から明らかであり、(2)が証明されれば、(3)も証明される。(2)については、下記のような
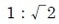 白銀長方形の図において、CEとEFの比率が、
白銀長方形の図において、CEとEFの比率が、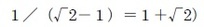 となることから証明される。
となることから証明される。
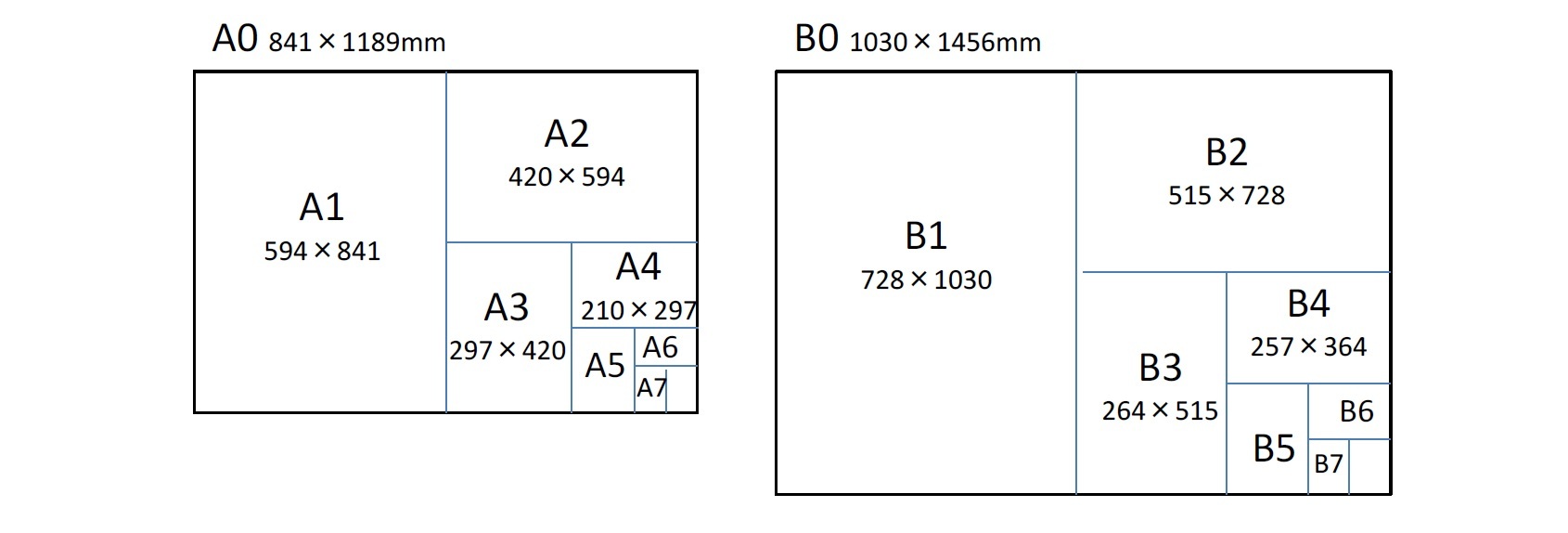
白銀比の使用例
1 A版は、もともとはドイツの工業規格だったものが国際規格(ISO 216)になり広く使われるようになった世界標準の紙のサイズであるのに対して、B版は江戸時代の公用紙の美濃判がルーツとなっている。
建築
法隆寺の金堂における1階の屋根と2階の屋根の長さが白銀比になっており、五重塔の最上階の屋根と最下層の屋根の長さがはやはり白銀比になっていると言われている。また、銀閣寺の1階と2階の横幅がほぼ白銀比になっているようだ。さらには、最近の建築物では、東京都墨田区にある「スカイツリー」が、全高が634m、第二展望台までの高さが448mとなっており、これを比率にすると1.415となり、ほぼ白銀比となっている。
法隆寺の金堂における1階の屋根と2階の屋根の長さが白銀比になっており、五重塔の最上階の屋根と最下層の屋根の長さがはやはり白銀比になっていると言われている。また、銀閣寺の1階と2階の横幅がほぼ白銀比になっているようだ。さらには、最近の建築物では、東京都墨田区にある「スカイツリー」が、全高が634m、第二展望台までの高さが448mとなっており、これを比率にすると1.415となり、ほぼ白銀比となっている。
人気キャラクター
「デザインのための数学」(牟田 淳著)によると、多くの人気キャラクターが白銀比の長方形の枠に収まっているとのことである。具体的には、この本によると、「となりのトトロ」、「ドラえもん」、「ミッキーマウス」、「スヌーピー」、「ちびまる子ちゃん」等がこれに該当しているとのことであり、これらのキャラクターの横幅と身長の比率が「白銀比」に近い値になっているようである。
「デザインのための数学」(牟田 淳著)によると、多くの人気キャラクターが白銀比の長方形の枠に収まっているとのことである。具体的には、この本によると、「となりのトトロ」、「ドラえもん」、「ミッキーマウス」、「スヌーピー」、「ちびまる子ちゃん」等がこれに該当しているとのことであり、これらのキャラクターの横幅と身長の比率が「白銀比」に近い値になっているようである。
青銅比
白金比
第2黄金比
さらには、「第2黄金比」と呼ばれるものは、以下の比率である。黄金比に対して、さらに横の比率が1だけ長い比率であるが、これはφ2(=φ+1)に相当する比率となる。

これも理論上は均整の取れた比率と考えられているようだが、明示的にはあまり使用されていない。
ただし、以前に説明した黄金角(約137.5度)は、360度をこの第2黄金比で割った値となる。

これも理論上は均整の取れた比率と考えられているようだが、明示的にはあまり使用されていない。
ただし、以前に説明した黄金角(約137.5度)は、360度をこの第2黄金比で割った値となる。
その他の比率
ここまで、いろいろな縦横比の概念について紹介してきた。実は当然のことながら、これらの代表的なケースに該当しない縦横比を有しているケースも多くみられる。その中で、黄金比と白銀比の中間的な比率である1.5程度の比率(この比率に対しては、特別な名称は付与されていないようである)を有するものが数多くみられる。
例えば、官製はがきのサイズは、100×148mmでその縦横比は1.48となっている。また、パスネット等のサイズは85.0×57.5mmでその縦横比は1.478となっている。さらに、トランプのカードの大きさには2種類あるが、ブリッジサイズは約57×89mmで縦横比は1.56、ポーカーサイズは約63×88mmで縦横比は1.40となっている。
サッカーの試合場となるサッカーコートのサイズについては、一定の規格はあるものの必ずしも統一されているわけでないようだが、ワールドカップ等の場合、タッチラインの長さが100m~110mでゴールラインの長さが64m~75mで、コートの面積は7.140㎡となっている。これによれば、縦横比は1.4から1.7の範囲に収まることになるが、ほぼ1.5前後の比率のスタジアムが多いようである。
例えば、官製はがきのサイズは、100×148mmでその縦横比は1.48となっている。また、パスネット等のサイズは85.0×57.5mmでその縦横比は1.478となっている。さらに、トランプのカードの大きさには2種類あるが、ブリッジサイズは約57×89mmで縦横比は1.56、ポーカーサイズは約63×88mmで縦横比は1.40となっている。
サッカーの試合場となるサッカーコートのサイズについては、一定の規格はあるものの必ずしも統一されているわけでないようだが、ワールドカップ等の場合、タッチラインの長さが100m~110mでゴールラインの長さが64m~75mで、コートの面積は7.140㎡となっている。これによれば、縦横比は1.4から1.7の範囲に収まることになるが、ほぼ1.5前後の比率のスタジアムが多いようである。
最後に
今回は、「黄金比」のより一般的な概念である「貴金属比」のうちの「白銀比」等について紹介してきた。各種の比率を紹介してきたが、結局は「黄金比」や「白銀比」が現実の世界では幅広く使用されてきているようである。また、今回はあくまでも長方形を対象に考えてきたので敢えて触れていないが、1:1の比率である正方形が幅広い場面で使用されていることは言うまでもない。
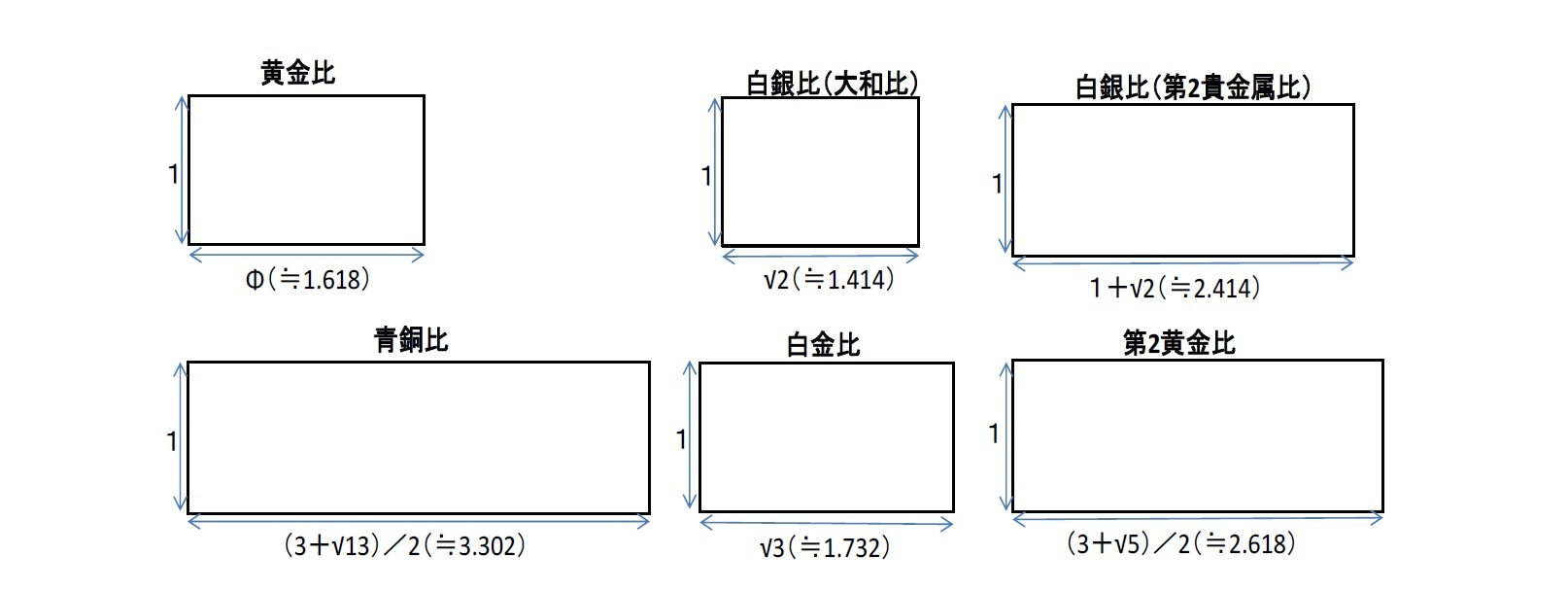
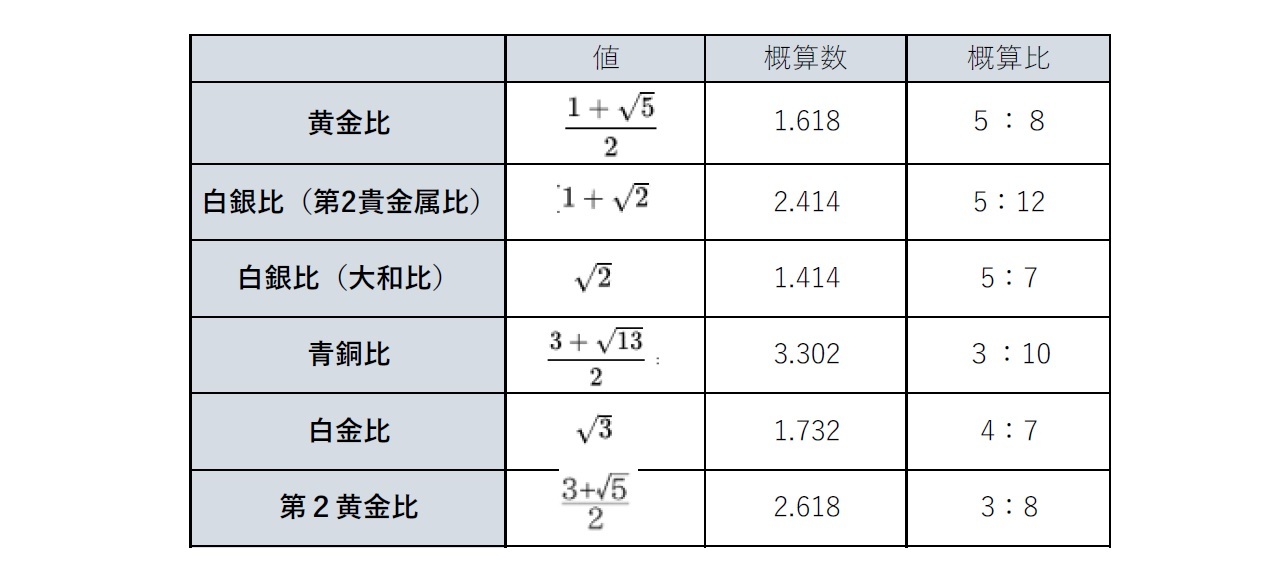
ここで、各比率に基づく長方形を掲載すると、以下の通りとなっている。
どの比率を最も快いものと感じるかは、個人によっても、またおそらくその使用用途によっても異なってくるものと思われる。今後何らかの図形等のデザインを考える際や、建築物や絵画等の芸術作品を鑑賞する際には、こうした典型的な比率を念頭に置いて、いろいろと考えてみるのも大変有用で興味深いのではないかと思われるが、いかがであろうか。
ここで、各比率に基づく長方形を掲載すると、以下の通りとなっている。
どの比率を最も快いものと感じるかは、個人によっても、またおそらくその使用用途によっても異なってくるものと思われる。今後何らかの図形等のデザインを考える際や、建築物や絵画等の芸術作品を鑑賞する際には、こうした典型的な比率を念頭に置いて、いろいろと考えてみるのも大変有用で興味深いのではないかと思われるが、いかがであろうか。
(2020年12月14日「研究員の眼」)
中村 亮一のレポート
| 日付 | タイトル | 執筆者 | 媒体 |
|---|---|---|---|
| 2025/11/04 | 数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- | 中村 亮一 | 研究員の眼 |
| 2025/10/23 | EIOPAがソルベンシーIIのレビューに関する技術基準とガイドラインのセットの新たな協議を開始等 | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/16 | EIOPAが2026年のワークプログラムと戦略的監督上の優先事項を公表-テーマ毎の活動計画等が明らかに- | 中村 亮一 | 保険・年金フォーカス |
| 2025/10/09 | 曲線にはどんな種類があって、どう社会に役立っているのか(その13)-3次曲線(アーネシの曲線・シッソイド等)- | 中村 亮一 | 研究員の眼 |
新着記事
-
2025年11月04日
数字の「26」に関わる各種の話題-26という数字で思い浮かべる例は少ないと思われるが- -
2025年11月04日
ユーロ圏消費者物価(25年10月)-2%目標に沿った推移が継続 -
2025年11月04日
米国個人年金販売額は2025年上半期も過去最高記録を更新-但し保有残高純増は別の課題- -
2025年11月04日
パワーカップル世帯の動向(2)家庭と働き方~DINKS・子育て・ポスト子育て、制度と夫婦協働が支える -
2025年11月04日
「ブルー寄付」という選択肢-個人の寄付が果たす、資金流入の突破口
お知らせ
-
2025年07月01日
News Release
-
2025年06月06日
News Release
-
2025年04月02日
News Release
【白銀比τ等について-白銀比とはどのようなもので、どんな場面で使用されているのか-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
白銀比τ等について-白銀比とはどのようなもので、どんな場面で使用されているのか-のレポート Topへ


















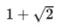
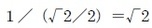
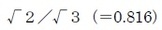


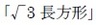
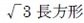
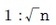
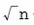

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!




