- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 数学記号の由来について(8)-「数」を表す記号-
コラム
2021年10月29日
はじめに
何回かに分けて、これまで慣れ親しんできた数学で使用されている記号の由来について、報告している1。
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回は、無限大(∞)、比例(∝)、相似(∽)等、第7回は、三角関数(sin、cos、tan等)について報告した。
今回は、「数」を表す記号の使用及び由来について報告する。
1 主として、以下の文献を参考にしてきている。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
第1回目は、四則演算の記号(+、-、×、÷)の由来について、第2回目は、数字の関係を表す記号(=、≒、<、>等)について、第3回目は、集合論で使用される記号(∩、∪、⊂、⊃等)について、第4回目は、論理記号(∀、∃、∴、∵等)、第5回は、べき乗(an)、平行根(√) 等、第6回は、無限大(∞)、比例(∝)、相似(∽)等、第7回は、三角関数(sin、cos、tan等)について報告した。
今回は、「数」を表す記号の使用及び由来について報告する。
1 主として、以下の文献を参考にしてきている。
Florian Cajori「A History of Mathematical Notations」(1928、1929)の冊子の再発行版(2012)(Dover Publications,Inc)
「N」(自然数)の使用及び由来
「N」は「自然数」を表しているが、これは英語の「Natural number」から来ている。正の整数のことを「自然数」というが、この名称は、正の整数が、我々が日常生活において物の個数を数える時に幅広く使用している最も身近なものであることから、「自然(Natural)」との感覚にマッチしていることによるものと思われる。なお、実際の表記においては、特に出版物等においては「黒板太字(中抜き文字あるいは重ね打ち体として言及される)」を用いて、「ℕ」と表されることも多い。この記号は、イタリアの数学者のジュゼッペ・ペアノ(Giuseppe Peano)によって1895年に最初に使用されたようだ。
19世紀のドイツの数学者レオポルト・クロネッカー(Leopold Kronecker)は「整数は神が作ったものだが、残りの数は人間が作ったものである(Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk)」という言葉を残しており、正の整数が自然な数と考えられて、自然数という用語が定着したようである。
また、「自然数」というのは、先に述べたように一般的には「正の整数」のことをいうが、集合論や論理学等では「0」を含めた「非負整数」を自然数と呼んだりする。「0」が含まれているかどうかを明確にするためには、「非負整数」や「正整数」という用語が使用されることもある。
19世紀のドイツの数学者レオポルト・クロネッカー(Leopold Kronecker)は「整数は神が作ったものだが、残りの数は人間が作ったものである(Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk)」という言葉を残しており、正の整数が自然な数と考えられて、自然数という用語が定着したようである。
また、「自然数」というのは、先に述べたように一般的には「正の整数」のことをいうが、集合論や論理学等では「0」を含めた「非負整数」を自然数と呼んだりする。「0」が含まれているかどうかを明確にするためには、「非負整数」や「正整数」という用語が使用されることもある。
「Z」(整数)の使用及び由来
「Z」は「整数」を表しているが、これはドイツ語で数を表す「Zahlen」あるいは整数を表す「GanzeZahl」から来ているとされている。英語では「Integer」(これは、英語で「whole」を意味するラテン語のintegerに由来している)2ということになるが、「I」は後で述べるように既に別の意味で使用されていたこともあり、「Z」の使用が普及していくことになったようだ。なお、同じく黒板文字では「ℤ」と表される。この記号は、「ランダウの記号O」で有名なドイツの数学者のエトムント・ランダウ(Edmund Landau)が1930年に最初に使用したようだ。
「整数」というのは、「自然数全体と0とマイナスの自然数全体」の集合ということになる。「整」という漢字は、「きちんとそろっている、半端が無い」という意味を有することから、小数点以下がない数として、この名称が付与されたものと思われる。
2 英語の「whole number」については、「counting number」として「自然数(正の整数)」や(0を含んだ)「自然数(非負整数)」を指す場合、「integer」として「整数」を指す場合等、国・地域等によっても異なる意味を有しているようだ。
「整数」というのは、「自然数全体と0とマイナスの自然数全体」の集合ということになる。「整」という漢字は、「きちんとそろっている、半端が無い」という意味を有することから、小数点以下がない数として、この名称が付与されたものと思われる。
2 英語の「whole number」については、「counting number」として「自然数(正の整数)」や(0を含んだ)「自然数(非負整数)」を指す場合、「integer」として「整数」を指す場合等、国・地域等によっても異なる意味を有しているようだ。
「Q」(有理数) の使用及び由来
「Q」は「有理数」を表している。「有理数」の英語名は「Rational number」であるが、「R」は以下に述べる「実数」で使用しており、英語の「(除算の)商(の整数部)」を意味する「Quotient」から「Q」を使用している。最初にジュゼッペ・ペアノによって1895年に「商」を意味するイタリア語quozienteに因んで表記されたことに由来しているとされている。なお、同じく黒板文字では「ℚ」と表される。
「有理数」というのは、「2つの整数a、b(≠ 0)を用いて、a/b という分数で表せる数」のことをいう(b = 1 とすることにより、任意の整数は有理数となる)。なお、このように「有理数」は分数の比で表せる数であり、「ratio」が「比」を意味するとして、「有比数」という訳語のほうが適切ではないかとの意見もある。
また、有理数を小数表示した場合には、「有限小数」又は「循環小数」となる。
「有理数」というのは、「2つの整数a、b(≠ 0)を用いて、a/b という分数で表せる数」のことをいう(b = 1 とすることにより、任意の整数は有理数となる)。なお、このように「有理数」は分数の比で表せる数であり、「ratio」が「比」を意味するとして、「有比数」という訳語のほうが適切ではないかとの意見もある。
また、有理数を小数表示した場合には、「有限小数」又は「循環小数」となる。
「R」(実数)の使用及び由来
「R」は「実数」を表しているが、これは英語の「Real number」から来ている。「Real」というのは、複素数の概念が導入された時の「虚数」(Imaginary number)に対応する言葉として導入されたものである。黒板文字では「ℝ」と表される。
実数の概念自体は、以前から存在していたが、例えば、実数論の基礎付けは、1872年にドイツの数学者であるリヒャルト・デデキント(Richard Dedekind)の「連続性と無理数」の中の、デデキント切断(Dedekind cutあるいはドイツ語で Schnitt) によって(無理数を定義することで)与えられた。それをここで説明すると、かなり複雑になってしまうと思われるので、ここでは述べない。
なお、実数を幾何学的に表示する方法として数直線があげられる。これは実数 0 に対応する原点とよばれる点を持った一つの直線で、直線上のそれぞれの点と原点との向きによる位置関係が各実数を表す形になっている。
実数の概念自体は、以前から存在していたが、例えば、実数論の基礎付けは、1872年にドイツの数学者であるリヒャルト・デデキント(Richard Dedekind)の「連続性と無理数」の中の、デデキント切断(Dedekind cutあるいはドイツ語で Schnitt) によって(無理数を定義することで)与えられた。それをここで説明すると、かなり複雑になってしまうと思われるので、ここでは述べない。
なお、実数を幾何学的に表示する方法として数直線があげられる。これは実数 0 に対応する原点とよばれる点を持った一つの直線で、直線上のそれぞれの点と原点との向きによる位置関係が各実数を表す形になっている。
「R―Q」(無理数)の使用及び由来
「R―Q」は「無理数」を表しており、英語では「Irrational number」と呼ばれる。これは有理数以外の実数であることから、「R」から「Q」を「除く」という意味で一般的な表記法である「-」を使用して「R-Q」(あるいは「R∖Q」やRにおける補集合と言う意味でcQ等)と表されている。
即ち、「無理数」というのは、「2つの整数a、b(≠ 0)を用いて、a/b という分数で表せない実数」を指している。有理数は加算個3であるのに対して、無理数は非加算個であり、殆どの実数は無理数、ということになる。
学生時代に学んだように、有名な無理数としては、例えば以下のような数が挙げられる。
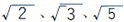 等(より一般的に「平方数でない数の平方根」等も無理数)
等(より一般的に「平方数でない数の平方根」等も無理数)
log2 、log3 等
円周率 π
ネイピア数 e
なお、πやeは、以前の研究員の眼で述べたように、「超越数」と呼ばれるものに区分される。
無理数を小数で表すと、循環しない無限小数となる。
無理数自体の存在は、古代ギリシアの時代から知られていたようだが、例えば「ピタゴラスの定理」で有名なギリシアの数学者ピタゴラスは、無理数の存在を認めていなかったと言われている。
これまでのケースとは異なり、無理数を表す一文字の記号等はない。これは、無理数が単独で扱われる機会が少なく、あくまでも実数の中での有理数でない数として扱われることが多いことによるものと思われる。無理数は、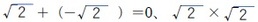 等、和や積に関して閉じていない(即ち、無理数の和や積が無理数になるとは限らない)というように、その代数的構造が弱い。従って、実数の中での有理数の補集合という位置付けでの記号で、特段の問題が発生していないものと思われる。
等、和や積に関して閉じていない(即ち、無理数の和や積が無理数になるとは限らない)というように、その代数的構造が弱い。従って、実数の中での有理数の補集合という位置付けでの記号で、特段の問題が発生していないものと思われる。
3 「可算(countable)」というのは、無限集合の全ての元と自然数の集合{1,2,3,…}との間に一対一対応がつけられることをいう。
即ち、「無理数」というのは、「2つの整数a、b(≠ 0)を用いて、a/b という分数で表せない実数」を指している。有理数は加算個3であるのに対して、無理数は非加算個であり、殆どの実数は無理数、ということになる。
学生時代に学んだように、有名な無理数としては、例えば以下のような数が挙げられる。
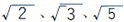 等(より一般的に「平方数でない数の平方根」等も無理数)
等(より一般的に「平方数でない数の平方根」等も無理数)log2 、log3 等
円周率 π
ネイピア数 e
なお、πやeは、以前の研究員の眼で述べたように、「超越数」と呼ばれるものに区分される。
無理数を小数で表すと、循環しない無限小数となる。
無理数自体の存在は、古代ギリシアの時代から知られていたようだが、例えば「ピタゴラスの定理」で有名なギリシアの数学者ピタゴラスは、無理数の存在を認めていなかったと言われている。
これまでのケースとは異なり、無理数を表す一文字の記号等はない。これは、無理数が単独で扱われる機会が少なく、あくまでも実数の中での有理数でない数として扱われることが多いことによるものと思われる。無理数は、
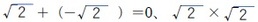 等、和や積に関して閉じていない(即ち、無理数の和や積が無理数になるとは限らない)というように、その代数的構造が弱い。従って、実数の中での有理数の補集合という位置付けでの記号で、特段の問題が発生していないものと思われる。
等、和や積に関して閉じていない(即ち、無理数の和や積が無理数になるとは限らない)というように、その代数的構造が弱い。従って、実数の中での有理数の補集合という位置付けでの記号で、特段の問題が発生していないものと思われる。
3 「可算(countable)」というのは、無限集合の全ての元と自然数の集合{1,2,3,…}との間に一対一対応がつけられることをいう。
「C」(複素数)、「I」(虚数) の使用及び由来
「C」は「複素数」を表しているが、これは英語の「Complex number」から来ている。黒板文字では「ℂ」と表される。米国の数学者ネイサン・ジェイコブソン(Nathan Jacobson)が1939年に最初に使用したようだ。
「複素数」というのは、「2つの実数 a, b と虚数単位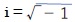 を用いて、z = a + bi と表すことのできる数」のことをいう。ここで「i」は虚数単位とよばれるもので、二乗すると-1になる数を表している。則ち
を用いて、z = a + bi と表すことのできる数」のことをいう。ここで「i」は虚数単位とよばれるもので、二乗すると-1になる数を表している。則ち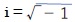 あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、これまで何度も紹介してきた米国の数学者、数学史家のフロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。
あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、これまで何度も紹介してきた米国の数学者、数学史家のフロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。
なお、b=0 の場合が実数であり、b ≠ 0 の場合には、実数でない複素数である「虚数」(imaginary number)となる。
「虚数」を発見したのは、16世紀のイタリアの数学者ジェロラモ・カルダーノ(Gerolamo Cardano)であるとされており、彼が発見した三次方程式の解の公式の中で、「虚数」の概念が導入されたようだ。その後、フランスの著名な哲学者・数学者であるルネ・デカルト(René Descartes)がその著書において、フランス語で「nombre imaginaire」(想像上の数)と名付けたことで、これが英語の「imaginary number」(虚数)の語源になった。これからわかるように、当時は0 や負の数ですら架空の仮想的なものと考えられていた時代で、ましてや「虚数」は否定的に捉えられていたようだ。
ドイツの数学者カール・フリードリヒ・ガウス(Carl Friedrich Gauß)は、複素数を平面上に表現する「複素数平面」(あるいは「複素平面」や「ガウス平面」とも呼ばれる)の概念を構築しているが、これについても「C」で表される。複素数平面上では、実軸を除いた部分が虚数全体となる。
なお、ガウスは1831年に発表した論文で、複素数を ドイツ語で「Komplexe Zahl」と表して、初めて複素数に名前を付けている。有名なガウスの「代数学の基本定理」は、「複素数を係数とする全てのn次方程式は、複素数の範囲でn個の解を有する」というものである。
因みに、日本における数学用語は、中国人の数学者が翻訳等して、中国に由来しているものも多いようだが、英語の「Complex number」を「複素数」と訳したのは、東京帝国大学教授であった藤沢利喜太郎博士で、1889年の著書『数学用語英和対訳字書』においてだった。藤沢利喜太郎博士は、日本の諸統計を用いて、日本で最初の日本人の生命表を作成して、生命保険業の発足や発展に貢献したことでも有名である。
「複素数」というのは、「2つの実数 a, b と虚数単位
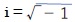 を用いて、z = a + bi と表すことのできる数」のことをいう。ここで「i」は虚数単位とよばれるもので、二乗すると-1になる数を表している。則ち
を用いて、z = a + bi と表すことのできる数」のことをいう。ここで「i」は虚数単位とよばれるもので、二乗すると-1になる数を表している。則ち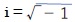 あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、これまで何度も紹介してきた米国の数学者、数学史家のフロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。
あるいは「i2=-1」となる。この「i」という文字が最初に使用されたのは、これまで何度も紹介してきた米国の数学者、数学史家のフロリアン・カジョリ(Florian Cajori)によれば、レオンハルト・オイラー(Leonhard Euler)による、1777年に提示され、1794年に公表された論文においてであったようだ。なお、b=0 の場合が実数であり、b ≠ 0 の場合には、実数でない複素数である「虚数」(imaginary number)となる。
「虚数」を発見したのは、16世紀のイタリアの数学者ジェロラモ・カルダーノ(Gerolamo Cardano)であるとされており、彼が発見した三次方程式の解の公式の中で、「虚数」の概念が導入されたようだ。その後、フランスの著名な哲学者・数学者であるルネ・デカルト(René Descartes)がその著書において、フランス語で「nombre imaginaire」(想像上の数)と名付けたことで、これが英語の「imaginary number」(虚数)の語源になった。これからわかるように、当時は0 や負の数ですら架空の仮想的なものと考えられていた時代で、ましてや「虚数」は否定的に捉えられていたようだ。
ドイツの数学者カール・フリードリヒ・ガウス(Carl Friedrich Gauß)は、複素数を平面上に表現する「複素数平面」(あるいは「複素平面」や「ガウス平面」とも呼ばれる)の概念を構築しているが、これについても「C」で表される。複素数平面上では、実軸を除いた部分が虚数全体となる。
なお、ガウスは1831年に発表した論文で、複素数を ドイツ語で「Komplexe Zahl」と表して、初めて複素数に名前を付けている。有名なガウスの「代数学の基本定理」は、「複素数を係数とする全てのn次方程式は、複素数の範囲でn個の解を有する」というものである。
因みに、日本における数学用語は、中国人の数学者が翻訳等して、中国に由来しているものも多いようだが、英語の「Complex number」を「複素数」と訳したのは、東京帝国大学教授であった藤沢利喜太郎博士で、1889年の著書『数学用語英和対訳字書』においてだった。藤沢利喜太郎博士は、日本の諸統計を用いて、日本で最初の日本人の生命表を作成して、生命保険業の発足や発展に貢献したことでも有名である。
最後に
今回は、「数」を表す記号の由来等について報告してきた。
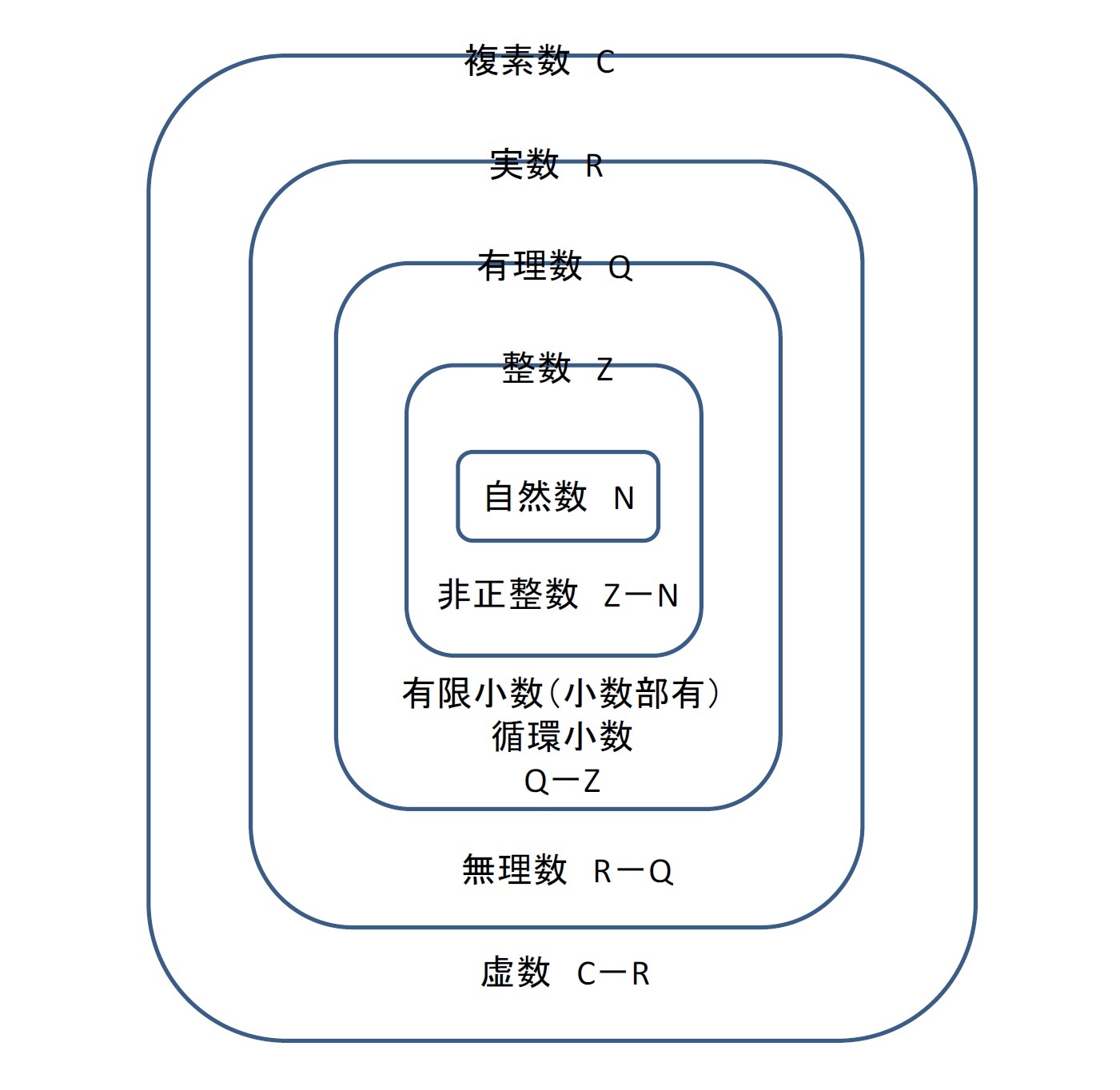
結局、これまで述べてきた数の構造は、以下の図の通りになっている4。
「数」を表す記号については、基本的にはそれを表す用語の頭文字に由来している。ただし、どの国の数学者がその「数」の研究等において、先導的・先駆的な役割を果たしてきたのか等によって、英語やドイツ語やイタリア語が語源になっている。さらに、これらの日本語等への翻訳については、それらの原語の意図するところを勘案した上で、適切と考えられる用語が使用され、普及してきたようである。
「数」を表す記号という基本的なものでさえ、昔から統一されたものがあったわけではなく、それぞれの経緯を経て、定着してきたものとなっている。グローバルに幅広く受け入れられ、使用されていく記号等の設定はそれほど容易ではないことがわかる。
結局、これまで述べてきた数の構造は、以下の図の通りになっている4。
「数」を表す記号については、基本的にはそれを表す用語の頭文字に由来している。ただし、どの国の数学者がその「数」の研究等において、先導的・先駆的な役割を果たしてきたのか等によって、英語やドイツ語やイタリア語が語源になっている。さらに、これらの日本語等への翻訳については、それらの原語の意図するところを勘案した上で、適切と考えられる用語が使用され、普及してきたようである。
「数」を表す記号という基本的なものでさえ、昔から統一されたものがあったわけではなく、それぞれの経緯を経て、定着してきたものとなっている。グローバルに幅広く受け入れられ、使用されていく記号等の設定はそれほど容易ではないことがわかる。
4 ここで述べたもの以外に、いくつかの数の分類があり、例えば以下のものが挙げられる。(1)自然数の中の「素数(prime number)」全体は、「P」や「ℙ」で表される。(2)複素数の中の「代数的数(algebraic number)」(複素数であって、有理数係数の 0 でない一変数多項式の根となるもの)全体は「A」等で表示され、複素数で代数的数でない数は「超越数」と呼ばれ、「C-―A」や「C/A」等で表される。
中村 亮一
研究・専門分野
(2021年10月29日「研究員の眼」)
公式SNSアカウント
新着レポートを随時お届け!日々の情報収集にぜひご活用ください。
新着記事
-
2024年04月19日
しぶといドル高圧力、一体いつまで続くのか?~マーケット・カルテ5月号 -
2024年04月19日
年金将来見通しの経済前提は、内閣府3シナリオにゼロ成長を追加-2024年夏に公表される将来見通しへの影響 -
2024年04月19日
パワーカップル世帯の動向-2023年で40万世帯、10年で2倍へ増加、子育て世帯が6割 -
2024年04月19日
消費者物価(全国24年3月)-コアCPIは24年度半ばまで2%台後半の伸びが続く見通し -
2024年04月19日
ふるさと納税のデフォルト使途-ふるさと納税の使途は誰が選択しているのか?
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2024年04月02日
News Release
-
2024年02月19日
News Release
-
2023年07月03日
News Release
【数学記号の由来について(8)-「数」を表す記号-】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
数学記号の由来について(8)-「数」を表す記号-のレポート Topへ


















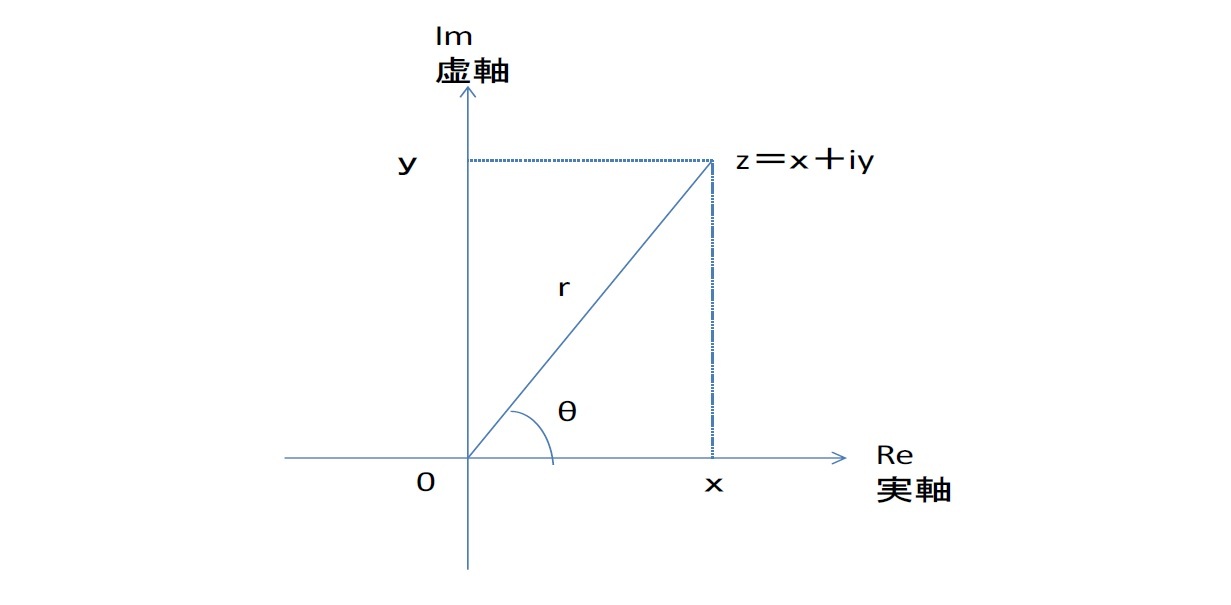

 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!





