逆正弦法則－ギャンブルで負けが込んでいる人は負け続ける?

保険研究部主席研究員兼気候変動リサーチセンターチーフ気候変動アナリスト兼ヘルスケアリサーチセンター主席研究員篠原拓也

このレポートの関連カテゴリ

確率や統計の話題には、ギャンブルと関係するものが多い。その中でも、コイン投げゲームにまつわるものは数多くある。コイン投げゲームの有名な法則を1つ紹介しよう。

まず、偏りのないコインを1枚用意する。コインを投げて表が出たら勝ち、裏が出たら負けとする。勝ちの場合は100円を受け取り、負けの場合は100円を支払う。このコイン投げを何度も繰り返す。コインを投げるごとに、100円を受け取ったり支払ったりするので累計収支が変動する。

コインに偏りがないとしているため、表と裏の出る確率はいずれも2分の1とみてよい。まず、最終的な累計収支がどのように分布するかを考えてみよう。最終的な累計収支がトントンになるケースは、たくさんある。当初勝ち続けて黒字が膨らんだが、その後負け続けて結局0になるケース。逆に、当初負け続けて大赤字になったが、その後勝ち続けて0に戻すケース。勝ったり負けたりを続けて0になるケースなどだ。勝ち続けたり負け続けたりして、大きな黒字や赤字になるケースは少ない。最終的な累計収支の分布は、収支0を頂点とした山の形になる。コインを10回投げる場合でみてみよう。

収支の変動パターンは全部で1,024 (=2の10乗) 通り。そのうち、最終的な累計収支が0のケースは252通り。一方10連勝や10連敗で、収支が1,000円の黒字や赤字となるケースは1通りしかない。

そこで、直感的に「勝っている状態(それまでの累計収支が、黒字の状態)と負けている状態(同、赤字の状態)は同じくらいある」という感じがしてくる。この直感は正しいだろうか。10回のコイン投げで、コインを１回投げるごとに、勝っている状態か、負けている状態かをみてみる。そして「黒字の状態の数－赤字の状態の数」として差をとる。これを1,024通りのそれぞれについて計算してみる。ただし、それまでの累計収支が0の状態は、黒字の状態や赤字の状態にはカウントしない。

10回とも裏の場合は、当然累計収支は常に赤字なので状態の差は-10。6回裏が出た後に4回表が出た場合も、ずっと赤字のため差は-10となる。3回裏が出た後に7回表が出た場合は、6回目が終わったところで累計収支は0。それまでの5回は赤字、それ以降の4回は黒字なので、差は-1となる。

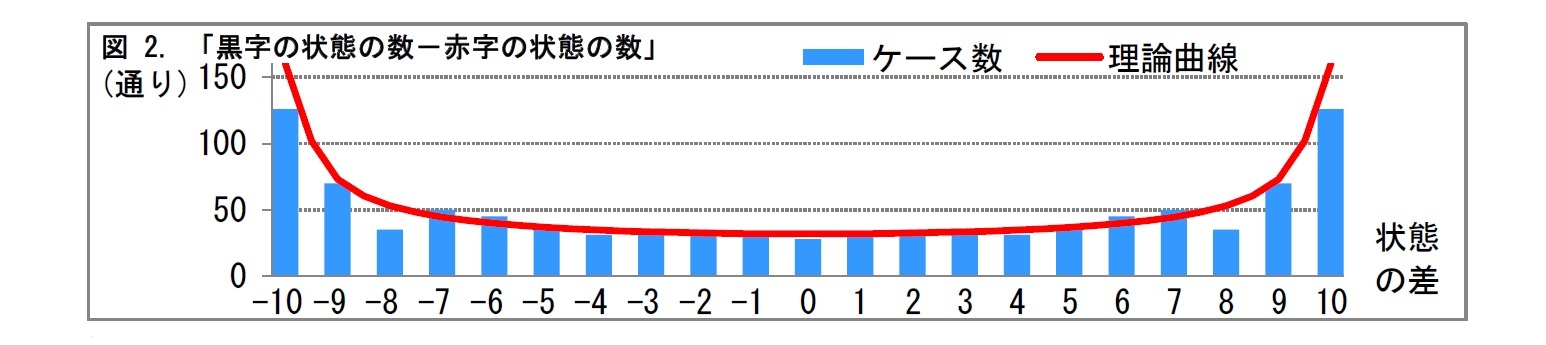
1,024通りについて「黒字の状態の数－赤字の状態の数」の差をまとめると、次のようになる。

直感に反して、図の両端、つまりずっと黒字の10や、ずっと赤字の-10のケースが多いのである。逆に、黒字と赤字の状態が同じになる、差が0のケースは一番少ない。つまり、「黒字と赤字のどちらかの状態に偏ることが多く、両方を同じくらいに経験することはあまりない」ということになる。

コインを投げる回数を10回よりも増やしていくと、U字型の理論曲線(赤線)に近づいていく。黒字と赤字の状態の差が一定範囲内にある確率を計算するには、この曲線の積分が必要となる。その際、逆正弦関数(サイン関数の逆関数)が現れる。このため、この事象は「逆正弦法則」と呼ばれている。

この法則を一般的な事例で理解するには、野球、バスケットボール、バレーボールなどのスポーツで、どれくらいシーソーゲームが起こりやすいかを考えてみるとイメージしやすい。対戦している両チームの実力が互角とすれば、点をとったり、とられたりする確率も同じくらいであろう。

では、試合がいつもシーソーゲームになるかというと、そうとは限らない。むしろ、先制点をあげたチームがそのまま逃げ切ることや、追いつかれて引き分けで終わることが多い。たとえ逆転劇が見られたとしても、逆転したチームがそのまま勝ち切ることが一般的だろう。両チームが逆転につぐ逆転の大熱戦を演じて観客を大いにわかせる、といった好ゲームにはめったにお目にかかれない。

コイン投げのゲームに話を戻そう。2つのことがわかった。累計収支の分布は収支0を頂点とした山の形になる(図1)。しかし、黒字の状態か赤字の状態かをみると、どちらかに偏る場合が多い(図2)。これは、すでに負けている状態からコイン投げゲームを始めた、と考えるとわかりやすい。たとえ少しくらい表が続いて出たとしても、負けている状態から脱するのは難しい。それどころか、もし裏が続いて出てしまえば、もっとひどい負けの状態に陥ることもある。つまり、ギャンブルで負けが込んでいる人は、今後も負け続ける可能性が高いといえる。

このコイン投げのゲームでは、表と裏の出る確率をいずれも2分の1ずつとして話を進めた。しかし、実際のギャンブルでは、勝ちと負けの確率が半々ということはあり得ない。ギャンブルの主催者に、ある程度利益が渡る仕組みとなっている。このため、ギャンブルのプレーヤーは1回のゲームでは負けることのほうが勝つことよりも多い、すなわち負けの確率は2分の1よりも大きいといえる。

ギャンブルで負けていると、それを取り返そうとして、さらにギャンブルにのめり込んでしまう。こういう話は昔からあちこちで耳にする。ギャンブルの行為や過程に心を奪われて、やめたくても、やめられない状態になる「ギャンブル依存症」の問題に、関係しているのかもしれない。

統計的には、赤字の状態から挽回して、同じくらいに黒字の状態を味わうことは起こりにくい。ギャンブルで負けているときには、いい加減どこかであきらめて、手を引く判断が必要と思われるが、いかがだろうか。

逆正弦法則－ギャンブルで負けが込んでいる人は負け続ける? | ニッセイ基礎研究所