ギリシアの3大作図問題－数学を通じて、ギリシアという国の歴史的位置付けの重みを再認識してみませんか

はじめに

ギリシアというと、昨今は債務問題で周囲の国に迷惑をかけている厄介な国だというイメージを持っている人が多いかもしれない。あるいは、それでも、古代ギリシアの遺跡やエーゲ海の美しい景色等から、観光として訪れたい国として引き続き良いイメージを持っている人も多いかもしれない。

古代ギリシアは、各種文明が発達し、その後の東西の文明に大きな影響を与えた国である。古代ギリシアにおいては、哲学者のソクラテスやプラトン等が有名だが、科学の分野においては、数学が特別な地位を占めており、何人かの有名な数学者がいた。おそらく最も有名なのは「ピタゴラスの定理」で有名なピタゴラスであろう。さらには、「アルキメデスの原理」で有名なアルキメデスや「ユークリッド幾何学」で有名なエウクレイデス（英語名でユークリッド）が挙げられる¹。

今回は、こうした古代ギリシアの時代の数学者たちによって問いかけられた有名な「ギリシアの3大作図問題」を紹介したい。

¹ 生誕地等で言えば、ピタゴラスはギリシアのサモス島、アルキメデスはイタリアのシチリア島のシラクサ、エウクレイデスはエジプトのアレクサンドリアである。

ギリシアの3大作図問題とは

「ギリシアの3大作図問題」とは、以下の３つの問題のことであり、2000年以上も解決されてこなかった問題である。

問題1（円積問題）：円と同じ面積を持つ正方形を作図する。

問題2（立方体倍積問題）：与えられた立方体の体積の2倍の体積を持つ立方体を作図する。

問題3（角の３等分問題）：任意の角を3等分する。

いずれの問題も極めてシンプルである。殆どの人がその内容を理解できる問題だと思われる。ところが、これが「作図」できるかどうかを証明することは大変難しい問題であった。

作図とは

ここで、「作図」とは、「定規とコンパスを使って作図」という意味である。現代であれば、コンピュータ等を使用して、簡単に作図できるが、「定規とコンパスを使って作図」ということになるとそうはいかなくなる。

「定規とコンパスを使って作図」とは、(1)定規は2点を直線で結ぶ（目盛りは使わない）、(2)コンパスは円を描く、(3)あくまでも手順は有限回である、ということを意味している。

さらには、「作図可能」とは、全ての角において作図可能ということであり、例えば、直角( 90度)のような特定のケースだけ、作図可能であっても答えにはならない。

その答えは

実は、答えは全て「作図不可能」ということになる。

これらの「作図不可能」性については、問題2（立方体倍積問題）と問題3（角の３等分問題）が1837年に、フランス人数学者ピエール・ローラン・ヴァンツェル（Pierre Laurent Wantzel）によって解決され、問題1（円積問題）については、1882年にドイツ人数学者フェルディナント・フォン・リンデマン（Carl Louis Ferdinand von Lindemann）によって解決された。

作図可能であるための条件

この初等幾何学の問題を解くためには、抽象代数学が使用されている。「抽象代数学」って何やそれ、と思う人が殆どだと思うが、「群」、「環」、「体」といった概念を取り扱う学問だ。

それでも、「群」、「環」、「体」って何やそれ、ということになると思うが、抽象代数学の概念の説明や作図不可能性の証明の詳細について興味のある方は専門書を参照してもらうことにして、ここでは作図不可能性についての非常に粗い説明をすることにする。専門家の人にとっては、あまりにもいい加減だと指摘されるかもしれないが、ご容赦いただきたい。

「定規とコンパスを使って作図可能」であることを示すためには、例えば、2次元平面の座標軸上で作図のために必要な点を（a、b）というような形で表現した場合に、これらのaやb といった数に対応する点を作図で示すことができる、ということを示す必要がある。

定規とコンパスを先に述べた方法で使用して作成できる点は、(1)直線と直線の交点、(2)直線と円の交点、(3)円と円の交点、の3種類である。座標平面上で、直線は1次方程式で、円は2次方程式で表される。　

こうしたことから、作図可能な数であるためには、「作図可能な数で表された1次方程式又は2次方程式の解として得られる数（それらの四則演算や平方根の結果として得られる数を含む）である」という条件が必要になる、ことが示される。

即ち、定規とコンパスによって作図可能となるには、作図のために必要な点が、（作図可能な数で表された）1次方程式や2次方程式を繰り返し解いて得られる範囲にあることが必要で、そのような条件を満たさない点がある場合には、作図不可能ということになる。

3大作図問題のケース

以上を「ギリシアの3大作図問題」に当てはめてみると、以下の通りとなる。

問題1（円積問題）
半径１の円の面積はπ（円周率）なので、この円と同じ面積を持つ正方形の1辺の長さは

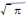となる。ここで、πは超越数といって、どんな有理係数の代数方程式の解にもならない数であることが先のリンデマンによって証明されたので、これは上記の条件を満たしていないということになる。

問題2（立方体倍積問題）
与えられた立方体の1辺の長さを１とすると、求めたい立方体の１辺の長さｘは、
　　　　X³=2
ということになるが、これは3次方程式であることから、上記の条件を満たしていない。

問題3（角の３等分問題）
与えられた角をθとすると、cos（θ／3）が分かれば、そこから直線を立てて、半径1の円との交点を求めることで、角を3等分できることになる。

A=cos θ、 X＝cos（θ／3）とすると、cosの3倍角の公式（高校の数学で学んだ記憶がある人もあると思われる）により、
　　　　４X³－3X－A＝0
となる。これも3次方程式であることから、上記の条件を満たしていない。

まとめ

このように、今から考えても、素朴に感じられる簡単な疑問や質問が、古代ギリシアの数学者に始まって、多くの人の興味・関心を呼び、長きにわたって、その解明に向けての研究が行われてきた。

それが、2000年の時を経て、新たな数学の概念を構築していくことを通じて、現代になってやっと解決された形になっている。「作図可能性」→「座標軸上の作図可能数」→「2次方程式での解」等といったプロセスを経て、幾何学の問題が代数学の問題に転化され、問題の明確化・構造化が行われ、解明が行われていったことになる。

数学とは本当に奥深い学問であるということとともに、ギリシアという国の歴史的な位置付けの重みを再認識させられた気がする。