- シンクタンクならニッセイ基礎研究所 >
- 保険 >
- 保険計理 >
- 回帰分析の落とし穴-分析結果は、推論の正しさを裏付けているか?
回帰分析の落とし穴-分析結果は、推論の正しさを裏付けているか?

保険研究部 主席研究員 兼 気候変動リサーチセンター チーフ気候変動アナリスト 兼 ヘルスケアリサーチセンター 主席研究員 篠原 拓也
実験や観測、アンケートなどから得られるデータをもとに、○○が原因で、□□という結果になる、という推論をしたとしよう。例えば、よく使われる例で、身長と体重の関係がある。ある成人男性の集団をもとに、「身長が高い人は、体重が重い」という推論をする。横軸に身長を、縦軸に体重をとって分布図として、各データを表してみると大体の傾向がわかる。体格は人それぞれで、中には、身長は高いが体重は軽いという人や、身長は低いが体重が重いという人もいるが、一般的には大きな体の人は小さな体の人に比べて身長が高く体重は重い、という傾向にあり、「身長が高い人は、体重が重い」という推論は、概ね間違っていないと考えられる。
それを図示するのに用いられるのが、回帰分析である。統計的な手法を用いて、分布図に、データの分布傾向を示す直線を引く。この線が右上がりの場合、身長が高いと体重が重い、という関係が見えてくる。
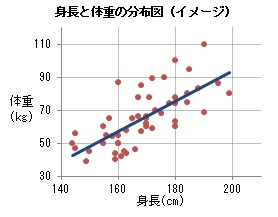
この直線と各データの間のずれが小さいほど、当てはまりのよい直線が引けることになる。横軸と縦軸の相関の程度は、相関係数という、1から-1までの間の数値で表される。正の値の場合、一方の数量が増えると、もう一方の数量も増えるという正の相関となる。身長と体重の関係は、正の相関である。逆に、一方の数量が増えると、もう一方の数量が減る場合は、負の相関となる。相関係数の値が1や-1に近いときは相関が強い、0に近いときは相関が弱いと言われる。
現在、回帰分析は、表計算ソフトや各種統計ツールで簡単に行うことができ、様々な統計分析で活用されている。しかし、回帰分析には、気をつけておくべき落とし穴がいくつか潜んでいる。
まず、1つ目は、データを区分すればするほど相関は強くなるが、結果が複雑になる点である。例えば、身長と体重の例で、集団を20~39歳、40~59歳、60歳~、などと年齢ごとの群団に分けて、それぞれ回帰分析をすると、群団に分ける前よりも、相関を強めることができる。これは一見、良いことのように見える。しかし、分析結果が複数に分かれて、複雑になることに注意する必要がある。ここで更に、各年齢群団を、肥満にならないよう食事制限や運動に努めている人と、そうではない人に分けて、それぞれのグループで回帰分析をすれば、もっと強い相関が得られるかもしれない。しかし、このようにして、区分を細かくして得られた分析結果は、複雑で理解しにくい。
2つ目は、原因と結果を逆にすると、奇妙な推論になってしまう点である。回帰分析は、両者の関係を直線で表示するが、因果関係については何も示さない。例えば、様々な都市で、警察官の数と犯罪率の関係を見てみると、両者には負の相関がある。これを、「警察官が多いと、犯罪率は低下する」と推論するのは妥当であろう。しかし、「犯罪率が低いと、警察官は多くなる」と推論するのは奇妙である。
3つ目は、無理やりに直線を当てはめても意味がない点である。野球の試合での控え投手を例に、ブルペンでの投球数と、試合での投球結果の関係を考えてみよう。控え投手は、ある程度プルペンで投球をしないと試合でいい結果が出せないが、プルペンで投げ込み過ぎると疲労してしまい悪影響となる。つまり、プルペンでの投球数と、試合での投球結果の関係を、単純な直線で表すことはできない。このような場合には、直線にこだわらずに、曲線で近似することを模索すべきであろう。
4つ目は、回帰分析は有効なツールだが、これだけで無理に推論を進めるべきではないという点である。例えば、2000年代に、日本の65歳以上人口と、アメリカの携帯電話契約数はいずれも増加した。回帰分析をすると、両者には、強い正の相関が見られることとなる。しかし、だからと言って、「2000年代は、日本の65歳以降の人口が上昇したから、アメリカの携帯電話の契約数が伸びた」などと推論することは、ナンセンスであろう。
最後に、5つ目の点は、応用編で、複数の原因を想定して分析をする場合に生じ得る「多重共線性」といわれる問題である。例として、先ほどの警察官の数と犯罪率に、パトカーの数も入れて、「警察官やパトカーの数が多いと、犯罪率は低下する」と推論してみよう。これは重回帰分析といわれ、犯罪率を、警察官とパトカーの数を用いた算式で、より精緻に表現しようとするものである。
ここで、「パトカーの数が多いと、犯罪率は上昇する」という分析結果が得られることがある。これは、原因として想定した、警察官の数と、パトカーの数の間に強い相関がある場合に発生する。算式上、「警察官の数が多いと、犯罪率は低下する」という関係が強く出過ぎてしまい、パトカーの数と犯罪率の関係が、これを打ち消すように、本来とは逆の関係として表現されてしまうのである。この場合、例えば警察官の数を除いて、パトカーの数と犯罪率の関係を、再度分析することが必要となろう。
以上のとおり、回帰分析には落とし穴がある。常に、データの分布図を参照して、分析結果の妥当性を確認する必要がある。また、回帰分析は推論を裏付ける証拠の1つにはなり得るが、回帰分析だけで推論の正しさが証明できる訳ではない。回帰分析を用いた分析結果を把握する際には、これらのことに注意する必要があると思われるが、いかがだろうか。

保険研究部 主席研究員 兼 気候変動リサーチセンター チーフ気候変動アナリスト 兼 ヘルスケアリサーチセンター 主席研究員
篠原 拓也 (しのはら たくや)
研究・専門分野
保険商品・計理、共済計理人・コンサルティング業務
03-3512-1823
- 【職歴】
1992年 日本生命保険相互会社入社
2014年 ニッセイ基礎研究所へ
【加入団体等】
・日本アクチュアリー会 正会員
(2015年03月16日「研究員の眼」)
公式SNSアカウント
新着レポートを随時お届け!日々の情報収集にぜひご活用ください。
新着記事
-
2024年04月23日
他国との再保険の監督に関する留意事項の検討(欧州)-EIOPAの声明 -
2024年04月23日
気候変動-温暖化の情報提示-気候変動問題の科学の専門家は“ドラマが少ない方向に誤る?” -
2024年04月23日
今後お金をかけたいもの・金融資産 -
2024年04月23日
今週のレポート・コラムまとめ【4/16-4/22発行分】 -
2024年04月22日
2024年3月、グローバル株式市場は上昇が継続
レポート紹介
-
研究領域
-
経済
-
金融・為替
-
資産運用・資産形成
-
年金
-
社会保障制度
-
保険
-
不動産
-
経営・ビジネス
-
暮らし
-
ジェロントロジー(高齢社会総合研究)
-
医療・介護・健康・ヘルスケア
-
政策提言
-
-
注目テーマ・キーワード
-
統計・指標・重要イベント
-
媒体
- アクセスランキング
お知らせ
-
2024年04月02日
News Release
-
2024年02月19日
News Release
-
2023年07月03日
News Release
【回帰分析の落とし穴-分析結果は、推論の正しさを裏付けているか?】【シンクタンク】ニッセイ基礎研究所は、保険・年金・社会保障、経済・金融・不動産、暮らし・高齢社会、経営・ビジネスなどの各専門領域の研究員を抱え、様々な情報提供を行っています。
回帰分析の落とし穴-分析結果は、推論の正しさを裏付けているか?のレポート Topへ


















 各種レポート配信をメールでお知らせ。読み逃しを防ぎます!
各種レポート配信をメールでお知らせ。読み逃しを防ぎます!





